Зміст законів збереження. Рівняння руху і закони збереження. Закон збереження імпульсу. Закон збереження моменту імпульсу.
4.1. Закони збереження дозволяють розглядати загальні властивості руху без розв`язку рівнянь руху і детальної інформації про розвиток процесів в часі.
4.2. Закони збереження відповідають на питання про те, що в послідовності фізичних ситуацій, які описуються рівняннями руху, залишається незмінним, постійним.
4.3. В законах збереження маємо не більше інформації, ніж в рівняннях руху. Проте в рівняннях руху необхідна інформація утримується в настільки неявному вигляді, що виділити її тяжко. За допомогою законів збереження ця інформація представляється нам в зручному й доступному вигляді.
4.4. В механіці закони збереження, в математичному їх розумінні, зводяться до перших інтегралів руху системи. Робота сили. Кінетична та потенціальна енергії. Поле сил. Потенціальні сили. Зв’язок між силою та потенціальною енергією. Потенціальний бар’єр. Закон збереження енергії.
4.5. Елементарною роботою сили F при переміщенні dr називається їх скалярний добуток dA=(F× dr), що в свою чергу дорівнює добутку цього переміщення на проекцію сили на нього.
4.6. Якщо скласти всі елементарні роботи, що виконуються при переміщенні по
контуру L, то ми отримаємо криволінійний інтеграл, що, за означенням, дорівнює
роботі по переміщенню вздовж контуру L:
4.7. Одиницею роботи в системі СІ є джоуль (Дж) – це робота сили в один Ньютон (1 Н) по здійсненню переміщення в 1 м у напрямку, який співпадає з напрямком сили.
4.8. Робота, виконана за одиницю часу називається потужністю
4.9. Якщо під дією сили змінюється модуль швидкості, то ця сила здійснює роботу.
4.10. Величина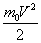 
називається
кінетичною енергією точки.
4.11. Робота сили по переміщенню матеріальної точки дорівнює приросту кінетичної енергії цієї точки.
4.12. Зміна кінетичної енергії матеріальної точки при її переміщенні між двома положеннями дорівнює роботі, здійсненій при цьому силою.
4.13. Сили, робота яких залежить лише від положення початкової і кінцевої точок траєкторії, але не від її вигляду, звуться потенціальними.
4.14. Простір, в кожній точці якого діють сили одного виду, називається полем сил. Поле потенціальних сил називається потенціальним – в ньому робота сил по замкненому контуру дорівнює нулю.
4.15. Сила називається центральною, якщо вона скрізь напрямлена до (від) однієї і тієї ж точки, яка називається силовим центром.
4.16. У випадку, коли робота сил поля не залежить від траєкторії, а залежить лише від положення початкової та кінцевої точок, кожній точці поля можна поставити у відповідність значення деякої функції U(x,y,z) такої, що різниця значень цієї функції в точках 1 та 2 буде визначати роботу сил по переміщенню з першої точки в другу: A12=U1-U2.
4.17. За допомогою функції U можна визначити роботу, яка здійснюється над частинкою при її переміщенні в полі потенціальних сил по будь-якому шляху між точками 1 і 2. Вона має розмірність енергії і називається потенціальною енергією.
4.18. Похідна функції U(x,y,z) по x
, що обчислена в припущенні, що змінні y і z
залишаються постійними, а змінюється лише x, називається частинною похідною
і позначається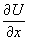 
.
4.19. Вектор з компонентами (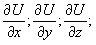
),
де U(x,y,z) – скалярна функція, називається градієнтом
функції U і позначається grad
U чи Ñ
U. Ці позначки еквівалентні.
4.20. Сила в потенціальному полі дорівнює градієнтові потенціальної енергії, який береться з протилежним знаком F= -Ñ U.
4.21. Величину Е, яка дорівнює сумі кінетичної і потенціальної енергій системи називають повною механічною енергією системи.
4.22. Якщо сторонні сили відсутні або такі, що не здійснюють роботи в той проміжку часу, який нас цікавить, то повна механічна енергія системи в полі цих сил залишається незмінною на даному проміжку часу.
4.23. Енергія не зникає і не з’являється, вона лише перетворюється з одного виду в інший.
4.24. Закон збереження енергії дозволяє провести порівняно простий аналіз загальних особливостей руху без детального знання рівнянь руху, якщо нам відомо закон зміни потенціалу ( потенціальної енергії ).
Потенціальний бар’єр. Потенціальна яма. Система матеріальних точок (СМТ). Центр мас. Закони збереження у неконсервативних системах. Закони збереження як наслідок симетрії простору та часу.
4.25. Системою матеріальних точок (СМТ) зветься сукупність скінченого їх числа, наприклад, газ в деякому об’ємі.
4.26. Сили, джерела яких лежать зовні системи, звуться зовнішніми.
4.27. Ізольована система – система матеріальних точок, на яку не діють зовнішні сили.
4.28. Сили з боку інших точок системи звуться внутрішніми.Звичайно приймають, що внутрішні сили задовольняють третьому закону Ньютона.
4.29. Імпульс ізольованої системи не змінюється при будь-яких процесах, які відбуваються всередині системи.
4.30. Момент імпульсу ізольованої системи не змінюється при будь-яких процесах, що відбуваються всередині системи.
4.31. В механіці Ньютона вимога про рівність нулю моменту внутрішніх сил СМТ приймається як постулат, який додається до законів Ньютона. Лише при цій умові можна вважати, що момент всіх сил зводиться до моменту зовнішніх сил.
4.32. Центральні сили залежать при даному характері руху лише від відстані між частинками і напрямлені по прямій, що з’єднує їх.
4.33.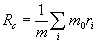 
– радіус-вектор, визначає
уявну точку, яка зветься центром мас системи.
За рухом центра мас можна слідкувати також як за рухом матеріальної точки.
4.34. Положення точки центру мас не залежить від системи, в якій воно визначається.
4.35. Рівняння руху СМТ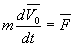 
еквівалентно
рівнянню руху матеріальної точки, вся маса якої зосереджена в центрі мас СМТ,
а всі сили, що діють на цю систему, діють ніби-то на неї.
4.36. Конфігурація системи – це відносне розміщення її частинок в даний момент.
4.37. Ми показали, що незалежно від системи відліку, робота всіх внутрішніх сил при переході частинок з одного положення в інше може бути представлена у вигляді зміни деякої функції, яка залежить при даному характері взаємодії від взаєморозміщення частинок системи, тобто від її конфігурації. Цю функцію називають власною потенціальною енергією системи (на відміну від зовнішньої потенціальної енергії, яка характеризує взаємодію даної системи з іншими тілами ).
4.38. Кожній конфігурації системи частинок властиве своє значення власної потенціальної
енергії і робота всіх центральних сил при зміні цієї конфігурації дорівнює зменшенню
власної потенціальної енергії системи:
Авнутр.=U1власн.-U2власн.
,
де U1власн. і U2власн.
– потенціальна енергія в початковому та кінцевому станах відповідно.
4.39. Кінетична енергія системи є величиною адитивною; вона дорівнює сумі кінетичних
енергій окремих частинок системи незалежно від того, взаємодіють вони поміж
собою чи ні. Приріст кінетичної енергії системи дорівнює роботі, яку здійснюють
всі сили, що діють на всі частинки системи:
К1-К2=А.
4.40. Дисипативними називаються такі сили, повна робота яких при будь-якому русі в замкненій системі від`ємна.
4.41. Приріст механічної енергії системи дорівнює алгебраїчній сумі робіт всіх
внутрішніх дисипативних та зовнішніх сил:
Е1-Е2=Авнутр.дис.+Азовн.
4.42. Механічна енергія замкненої системи частинок, в якій відсутні дисипативні
сили, зберігається в процесі руху:
Е=К+Uвласн.=const.
4.43. Механічна енергія може зберігатися і в незамкненій системі, якщо зменшення
енергії за рахунок роботи проти внутрішніх дисипативних сил компенсується надходженням
енергії за рахунок зовнішніх сил.
4.44. Енергія ні з чого не утворюється і не знищується, вона може лише переходити з однієї форми в іншу або від однієї частини матерії до іншої.
4.45. Справедливість ІІІ закону Ньютона і закону збереження імпульсу замкненої СМТ обумовлені однорідністю простору.
4.46. Під ізотропністю простору розуміють еквівалентність різних напрямків в просторі. Це означає, що якщо є деяка ізольована система, то розвиток подій в ній не залежить від того, як вона орієнтована в просторі.
4.47. Закон збереження моменту імпульсу ізольованої СМТ обумовлений ізотропністю простору в інерціальних системах відліку.
4.48. Під однорідністю часу розуміють еквівалентність різних моментів часу між собою. Це означає, що деяка фізична ситуація розвивається однаково незалежно від того, в який момент часу вона здійснюється.
4.49. Закон збереження енергії ізольованої СМТ зумовлений фундаментальною властивістю часу в інерціальних системах – його однорідністю.
Рух тіл змінної маси. Реактивний рух. Рівняння Мещерського. Формули Ціолковського. Визначення зіткнень та ударів. Пружні та непружні удари. Закони збереження при ударах. Розгляд співударів за допомогою векторних діаграм.
4.50. Реактивними називаються двигуни, тяга яких створюється за рахунок відкидання частини власної маси тіла, що рухається.
4.51. Зіткненням називається взаємодія двох чи більше тіл чи матеріальних точок, що проходить в відносно малій області простору за відносно малий проміжок часу так, що поза цією областю простору і поза цим проміжком часу рух тіл можна розглядати як такий, при якому тіла не взаємодіють.
4.52. Зіткнення (удар) – важливо, щоб область зіткнення (дотику) була мала порівняно з простором, в якому розглядається рух тіл до і після зіткнення, а час зіткнення – малий порівняно з часом спостерігання події до і після зіткнення.
4.53. Абсолютно пружнім називається такий удар, при якому механічна енергія не переходить в інші, немеханічні форми енергії.
4.54. Абсолютно непружний удар характеризується тим, що при ньому потенціальна енергія деформації переходить цілком в немеханічну форму енергії, а не назад в кінетичну енергію тіл, що стикаються. При цьому тіла, що зіткнулися абсолютно непружно, мають рівні швидкості як по модулю, так і по напрямку.
4.55. Удар називається центральним, якщо до удару тіла рухалися вздовж прямої, що з’єднує їх центри.
4.56. Прицільний параметр d d – відстань від центра кулі, що не рухається, до лінії руху кулі, що рухається.
Принцип відносності в механіці. Перетворення Галілея. Інерціальні системи відліку. Інваріанти перетворень: довжина, час, прискорення. Абсолютність одночасності. Додавання швидкостей.
4.57. Величини, числові значення яких не змінюються при перетвореннях координат, називаються інваріантами перетворень.
4.58. Довжиною рухомого стержня називається різниця координат його кінців в певний момент часу.
4.59. Принцип відносності Галілея