02-01. Хвильове рівняння, випадок поперечно-обмеженої системи.
Рівняння Максвела 2-ого порядку описують всі електромагнітні явища
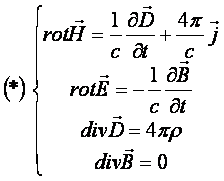 (1)де
(1)де ![]() - густина струму,
- густина струму, ![]() - напруженість ЕП,
- напруженість ЕП, ![]() - напруженість МП,
- напруженість МП, ![]() - індукція МП,
- індукція МП, ![]() - індукція ЕП,
- індукція ЕП, ![]() - густина заряду
- густина заряду
Хвильове рівняння:
![]() ; де
; де ![]() (2)
(2)
Із двох перших рівнянь Максвела (1) можна вивести хвильове рівняння із
врахуванням часової компоненти. Візьмемо ротор від обох частин першого рівняння
(1), а потім підставимо в нього значення для ![]() із другого
рівняння (1):
із другого
рівняння (1):
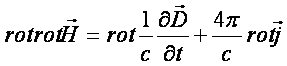 (3)
(3)
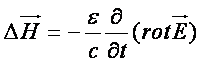 (4)
(4)
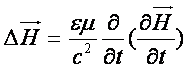 (5)
(5)
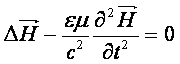 (6) - хвильове рівняння для просторової і часової
компоненти
(6) - хвильове рівняння для просторової і часової
компоненти
Порівняємо це із хвильовим рівнянням лише для просторової компоненти (2):
![]() (7)
(7)
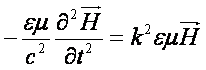 Підставимо
Підставимо ![]()
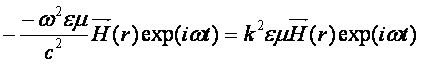
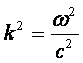 (другу частину
питання не на 100%, але мабуть мається на увазі що розглядаються хвилі вздовж
однієї осі, або те, що в поперечно-обмеженій системі виникають стоячі хвилі
вздовж цього напрямку)
(другу частину
питання не на 100%, але мабуть мається на увазі що розглядаються хвилі вздовж
однієї осі, або те, що в поперечно-обмеженій системі виникають стоячі хвилі
вздовж цього напрямку)
У плоскої хвилі на хвильовому фронті амплітуда і
фаза однакова. Нехай хвиля розповсюджується в напрямку ![]() , то
, то ![]() .Отримаємо
.Отримаємо 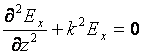 (з
(з ![]() ). Розв’язок отриманого рівняння осцилятора:
). Розв’язок отриманого рівняння осцилятора: ![]() .
.
Перейдемо до справжньої
компоненти поля: ![]() де
де ![]() - рівняння хвильового фронту (фаза
- рівняння хвильового фронту (фаза ![]() ). Цей фронт розповсюджується зліва направо. Якби ми
взяли замість
). Цей фронт розповсюджується зліва направо. Якби ми
взяли замість ![]() компоненту
компоненту ![]() , то одержали б
, то одержали б ![]() - фронт, що рухається справа наліво. Стояча хвиля – це
суперпозиція цих двох компонент.
- фронт, що рухається справа наліво. Стояча хвиля – це
суперпозиція цих двох компонент.
Розглянемо ![]() .
.
 .
.
![]() ;
; 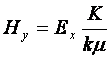 , тобто маємо дійсно праву трійку
, тобто маємо дійсно праву трійку ![]() . Оскільки
. Оскільки ![]() , то
, то  .
.
Таким чином у плоскій хвилі ![]() і
і ![]() залежні величини: якщо одне з них задане, то друге визначається
лише серидовищем (див. *). Це в СГСЕ, в інших
системах по іншому. Наприклад, в СІ у вакуумі
залежні величини: якщо одне з них задане, то друге визначається
лише серидовищем (див. *). Це в СГСЕ, в інших
системах по іншому. Наприклад, в СІ у вакуумі 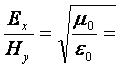 377 (Ом) – опір вільного простору (хвильовий опір
простору).
377 (Ом) – опір вільного простору (хвильовий опір
простору).