01-12. Зміна власних частот резонатора скінченною провідністю його стінок.

Якщо не враховувати провідність стінок резонатора та використовувати ідеальні граничні умови, то отримуємо незатухаючі коливання. Врахування кінцевої провідності стінок приводить до того, що вільні коливання в пустих резонаторах затухають, як наслідок втрат в стінках.

Внаслідок затухання частоти коливань являються комплексними , де - резонансна частота, а - має зміст коефіцієнта затухання. Це значить, що миттєві значення полів затухають по експоненційному закону (пропорційно ), а енергія електромагнітного поля в резонаторі – по закону: , 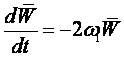(1). Знайдемо приблизне значення коефіцієнта затухання скориставшись законом збереження енергії та усереднивши по періоду коливання: 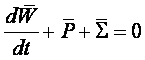(2). Цей закон зручно застосовувати до об’ємного резонатора V, обмеженному поверхнею стінки S. Струми в стінці розташовані поза об’ємом, тому . Поеднуючи формули (1) та (2) маємо коефіцієнт затухання у вигляді: 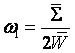. Величину - середню потужність, що витікає з об’єму в стінки резонатора, обрахуємо наближено за допомогою умови Леонтовича: , де t прирівнюється до тангенсійного магнітного поля на стінці ідеального резонатора.

Тоді маємо: , .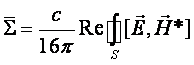

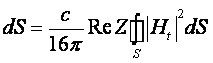Енергетична формула застосовується для наближених розрахунків, виходячи з тих полів, які знайдені в припущенні ідеального резонатора, до того ж вважаємо, що середнє значення електричної енергії рівне середньому значенню магнітної енергії: 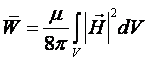. В результаті для коефіцієнта затухання маємо: 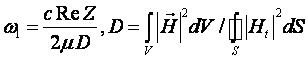. Виразимо хвильовий опір Z через глибину скін-шару d та, враховуючи, що провідність стінок велика, в результаті отримаємо : 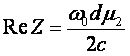. І остаточно .

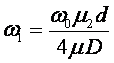Таким чином, отримуємо, що коефіцієнт затухання пропорційний глибині скін шару d та обернено пропорційний кореню з провідності ; пропорційний кореню з резонансної частоти (глибина скін-шару ).