02-03. Коаксіальна лінія

Тут можуть розповсюджуватись хвилі Т (бо тут можна утворити конденсатор), ТЕ, ТМ. , , .

.

Розглянемо хвилю Т. Нам необхідно розв’язати рівняння . Зробимо це методом конформних відображень. Його можна застосувати для аналітичних функцій (тих, що задовольняють рівнянню Лапласа), яким і є поле Т-хвиль.

Для того, щоб скористатись методом КВ, необхідно:

1. Знайти відображення, яке переводить нашу область, де існує ЕМ – поле, у плоский конденсатор;

2. Розв’язати рівняння Лапласа у плоскому конденсаторі;

3. 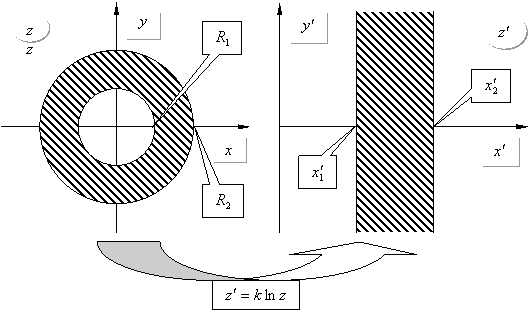Зворотнім конформним перетворенням знов перейти в нашу область – це і буде розв’язок задачі:

Метод конформних відображень можна застосувати для Т – хвилі, бо вона є розв’язком рівняння Лапласа: , . Доведемо, що відображення перетворює циліндричний конденсатор в плоский: , , тобто , . Таким чином, якщо . , .

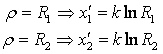Таким чином, можна перетворити межу циліндричної області в межу плоскої. Тому й область перетворюється в область . Розв’язок задачі в плоскому конденсаторі: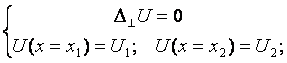має вигляд: 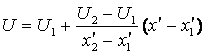. Поклавши (скориставшись тим, що потенціал визначається з точністю до константи), маємо: . Скориставшись зворотнім перетворенням, одержимо: .

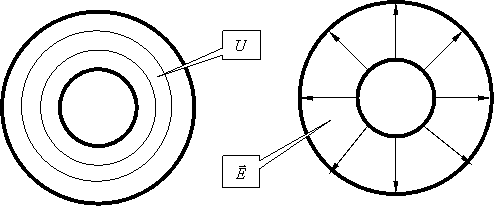
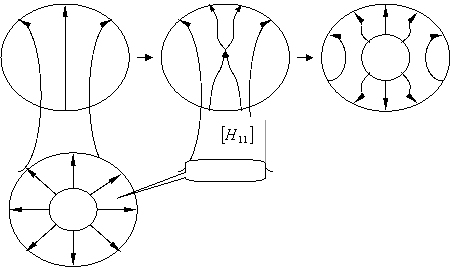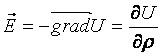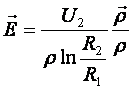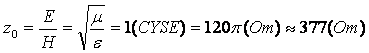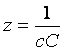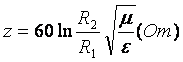Знайдемо поле: , . Хвильовий опір: . Проте такий опір не вимірюється. Більш практичне означення хвильового опору: - відношення напруг лінії до струмів у цій лінії. Знайдемо для Т – лінії, використавши інтегральні рівняння Максвела: , тут - заряд, - ємність на одиницю довжини. З урахуванням можна записати: . . Окрім Т – хвилі, в коаксіальному кабелі може існувати ще й ТЕ чи ТМ хвиля: .

Картина хвиль:

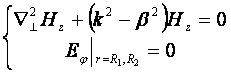. Наприклад, для R₁=1мм, R₂=6мм: .