5. Частотні властивості транзистора

5.1. Рух неосновних носіїв у базі. Перехідні процеси у транзисторі

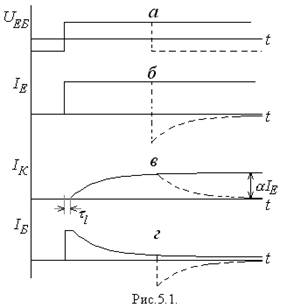
Вище, розглядаючи принцип дії біполярного транзистора, ми дійшли висновку, що колекторний струм створюється неосновними носіями, котрі були інжектовані в базу через емітерний перехід і в результаті дифузії через базу дістались до колекторного переходу. Звичайно, на дифузію через базу потрібний хоч і невеликий, але скінчений час. Тому, при cтрибкоподібному збільшенні емітерного струму  - транзистора, увімкненого за схемою СБ, колекторний струм зростає не одразу, а з. деяким запізненням. (рис.5.І). Якийсь час  колекторний струм взагалі відсутній - заряди ще не встигли дістатись до колектора. Потім, в міру того як хмаринка неосновних носіїв в наслідок дифузії досягає колектора, струм поступово зростає, прямуючи до усталеного значення. Середній час дифузії через базу дорівнює

де  - товщина бази,  - коефіцієнт дифузії неосновних носіїв в матеріалі бази. Так, наприклад, для дірок в кремнії  =13 см ²/с, отже при =1 мкм середній час дифузії дорівнюватиме 8.10 ^-10с. Саме цим часом і визначається темп зростання струму колектора. Час затримки    звичайно набагато менший від , тому ним можна нехтувати. Хід зростання колекторного струму досить добре апроксимується експоненціальним законом

                                                 (5.1)

При стрибкоподібному запиранні емітерного струму (пунктир на мал.5.16) колекторний струм припиняється не одразу, а спадає поступово, в міру розсмоктування (знову ж таки за рахунок дифузії) хмаринки неосновних носіїв, які накопичилися в базі. При цьому дифузія може йти не тільки у бік колектора, але й у бік емітера, який тепер також має запірну напругу. Тому в момент запирання емітерний струм змінює свій напрям і далі поступово зменшується. Процеси спаду емітерного та колекторного струмів також можна описати експоненціальним законом із сталою часу. В той момент, коли починається інжекція неосновних носіїв в базу, різко зростає базовий струм (рис.5.І,г). Причина такого зростання полягає у тому, що в міру надходження в базу неосновних носіїв, їх об’ємний заряд повинен компенсуватися зарядами протилежного знаку які надходять в базу з джерела живлення. Виходячи із співвідношення (3.2), яке повинно виконуватися в будь-який момент часу, базовий струм має змінюватися за законом

                                       (5.2)

З цієї формули випливає, що в перші моменти після увімкнення, базовий струм є сумірним з емітерним, тоді як в усталеному режимі він завжди набагато менший від останнього. Після припинення емітерного струму об’ємний заряд неосновних носіїв в базі розсмоктується і основні носії, котрі цей струм компенсували, тепер стікають, утворюючи екопоненціальний імпульс базового струму зворотної полярності.

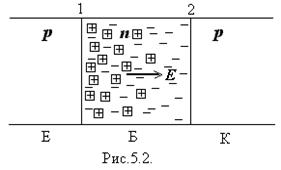
Щоб скоротити час руху неосновних носіїв, в об’ємі бази іноді створюють внутрішнє електричне поле, яке прискорює їх рух до колектора. Таке поле можна створити шляхом нерівномірного легування матеріалу бази. Так, наприклад, створивши в базі більш високу концентрацію донорних домішок в області емітерного переходу (рис.5.2; атоми донорніих домішок тут зображені кквадратиками з хрестиками), можна добитися такого стану, коли вільні електрони за рахунок дифузії більш або менш рівномірно розподіляться по об’єму бази, тоді як атоми домішку зостануться закріпленими в кристаличній гратці. Їх об’ємний заряд створює електричне поле Е, що прискорює ін-жектовані в базу дірки. Тепер рух дірок у базі відбуватиметься не тільки внаслідок дифузії, але й за рахунок дрейфу в електричному полі, яке "підганяє" їх у бік колектора.

Транзистори такого типу називають дрейфовими. За рахунок дрейфу можна скоротити час руху неосновних носіїв в базі в кілька разів порівняно з простою дифузією і тим самим істотно підвищити швидкодію транзистора.

5.2. Частотна залежність коефіцієнта передачі струму.

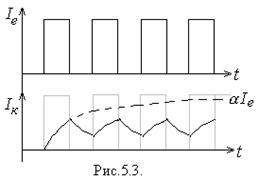
Якщо стрибкоподібні відкривання та запирання емітерного переходу відбуватимуться періодично з періодом, сумірним з , то колекторний струм кожного разу не встигатиме ані дорости до усталеного значення  , ані повністю зменшитись до нуля. Часова залежність колекторного струму  матиме вигляд пилкоподібних коливань (рис.5.З), розмах яких буде тим меншим, чим меншим стає відношення  .

Звідси випливає, що з підвищенням частоти вхідної (емітерної) напруги керуюча дія транзистора буде погіршуватись і коефіцієнт передачі струму  зменшуватиметься. Дійсно, чотириполюсник, в якому перехідні процеси опиcуютьcя  виразом виду (5.І), повинен мати таку частотну характеристику

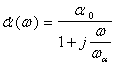                                           (5.3)

де: - значення коефіцієнту  на низьких частотах (а - гранична частота транзистора, увімкненого за схемою зі спільною базою. Адже перехідну функцію транзистора можна перетворити в його передавальну функцію (частотну характеристику) , застосувавши пряме Фур’є-перетворення. Залежність модуля коефіцієнта   від частоти описується виразом

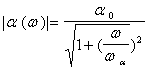                                   (5.4)    

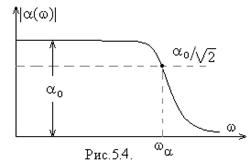
і подана на рис.5.4. З цього графіка видно, що модуль в досить широкому діапазоні низьких частот зберігається майже незмінним і рівним, а потім починає плавно зменшуватись, асимптотично наближаючись до нуля в  області високих частот.

5.3. Граничні частоти.

Неможливо, звичайно, точно вказати ту частоту, починаючи з якої транзистор втрачає свої підсилювальні властивості. Однак, можна умовно прийняти за неї таку частоту, для якої модуль  зменшується в порівнянні з  в разів. Ця частота має назву граничної частоти транзистора. Для розглянутого нами вище прикладу вона дорівнюватиме 1.25.10⁹с^-1 або 2.10⁸Гц. У довідниках цю частоту позначають як -

тобто як частоту, на якій параметр   - коефіцієнт передачі за струмом у схемі із спільною базою - зменшується в 0,71 разів (або на 3 дБ) порівняно з його значенням для низьких частот.

Вираз для частотної залежності коефіцієнта передачі  за струмом для схеми із спільним емітером можна одержати з виразу (3.4), підставивши туди замість його значення (5.3)

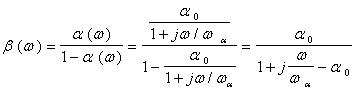
Розділивши чисельник і знаменник дробу на 1-матимемо:

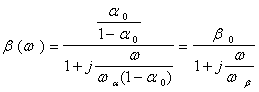                                           (5.5)

  Ця формула аналогічна (5.3). Величина  є коефіцієнтом передачі за струмом для схеми СЕ в області низьких частот, а - гранична частота для цієї схеми.

                                              (5.6)

Гранична частота значно менша граничної частоти  для схеми СБ. Так, наприклад, для розглянутого вище прикладу і при =50 частота   дорівнюватиме лише 4.І0⁶  Гц.

Фізичну причину погіршення частотних властивостей транзистора при його увімкненні за схемою СЕ можна зрозуміти з розгляду рис. 5.1г:  з малюнку видно, що при швидких перемиканнях базовий струм виявляється сумірним з емітерним, так що коефіцієнт  в ці моменти часу стає набагато меншим, аніж в стаціонарному (або низькочастотному) режимі. В довідниках гранична частота  позначається як  і від- повідає  частоті, на якій коефіцієнт передачі за струмом  у схемі СЕ   знижується на 3 дБ.

Частота, на котрій у схемі СЕ параметр  стає рівним одиниці (тобто транзистор втрачає підсилювальні властивості за струмом) позначається як  і має назву частоти одиничного підсилення. Звичайно  близька до граничної частоти для схеми із спільною базою і становить  (0.6 - 0.8).

Окрім перелічених вище граничних частот транзистор може бути охарактеризований ще і так званою максимальною частотою генерації . При цій частоті коефіцієнт підсилення транзистора за потужністю стає рівним одиниці і транзистор взагалі втрачає здатність до підсилення сигналів.

5.4. Фізична еквівалентна схема транзистора

в області високих частот

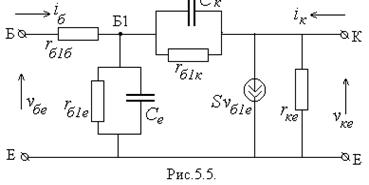
            Фізична еквівалентна схема транзистора в області високих зображена на рис.5.5. За прізвищем її автора цю схему іноді називають схемою Джіаколетто. У своїй вихідній частині схема Джіаколетто нагадує еквівалентну схему у g -параметрах (рис.4.З): джерело струму тут також зашунтоване вихідним опором . Однак, вхідна частина цієї схеми, побудова  зовсім інакше. Принципова відмінність еквівалентної схеми Дкіаколетто від раніше розглянутих полягає у тому, що в ній враховується поперечний опір бази. Нагадаємо, що база - це тонкий шар слабко легованого напівпровідника товщиною порядку І мкм при поперечних розмірах порядку І мм. Вивід бази, позначений літерою Б, знаходиться на периферії цього шару, тоді як всі процеси проходження струму обумовлені, в основному, його центральною частиною.          Так, наприклад, коли йдеться про напругу на емітерно-базовому переході, якою обумовлена величина струму , то треба мати на увазі різницю потенціалів між емітером і точкою БІ, яка знаходиться в центрі базового шару і яку надалі ми називатимемо "істиною базою". Ця напруга відрізняється від прикладеної до вводів Б та Е на вличину спаду напруги на поперечному опорі . Через слабку легованість бази та її малу товщину цей опір може бути  досить великим і досягати сотень, чи навіть тисяч Ом.

Тому роботою транзистора, точніше його колекторним струмом, в дійсності керуватиме не прикладена до вводів вхідна напруга , а та її частина, яка виявляється прикладеною між емітером та істиною базою - точкою Б1. Цей висновок і врахований у фізичній еквівалентній схемі, де джерело струму у колекторному колі керується саме напругою , а не. Нехтуючи, поки що,  відгалуженням струму через резистори  та ємністю можна записати

[1]                                                     (5.7)

де  - крутість прохідної характеристики транзистора. Оскільки , то її можна визначити як

                                                (5.8)

де  - диференціальний опір емітерно-базового переходу, визначений вище виразом (1.4).

Напруга  створюється внаслідок проходження базового струму через комплексний опір  , утворюваний паралельним сполученням резистора та ємності .

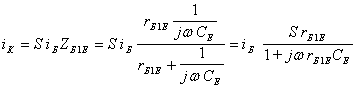                   (5.9)

            З цього виразу ясно видно, що колекторний струм (амплітуда його змінної частини   ) з підвищенням частоти зменшується, оскільки зростає шунтуюча дія ємності , і керуюча напруга  зменшується. Тим самим в еквівалентній схемі моделюються частотні властивості реального транзистора. Слід лише підібрати величини елементів еквівалентної схеми так, щоб досягти найкращого кількісного збігу.

 Вираз (5.9) за своєю структурою подібний до виразу (5.5), який можна переписати так: :

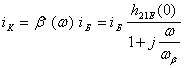                                                  (5.10)

Щоб еквівалентна схема мала такі ж  частотні властивості, як і реальний транзистор, слід прирівняти один одному відповідні члени виразів (5.9) і (5.10), а саме

Звідсі одразу ж визначаються елементи еквівалентної схеми      

                                         (5.11)

,                                                    (5.12)

де  - значення цього параметра на нульовій (низькій) частоті.

Вхідний опір транзистора на низьких частотах  , отже

                                                        (5.13)

Розглянемо тепер решту елементів еквівалентної схеми. Ємність є реально існуючою бар’єрною ємністю закритого колекторного переходу. Резистор моделює внутрішній зворотний зв’язок у транзисторі, який описується параметром  . У відповідності до (4.19а) можна записати

     при     та  .

Оскільки ж при  можна вважати, що = , то

                  звідки                   (5.14)

            Для вихідного кола, згідно до закону Кірхгофа, маємо

         (знову ж таки при      та  ).

Враховуючи, що   дістанемо

або нехтуючи останнім доданком (з причини дуже великих значень )

(5.15)

            Отже, таким шляхом елементи схеми Джіаколетто можна виразити через  - параметри транзистора та його граничну частоту .

5.5. Маркировка та класифікація транзисторів,

У відповідності з діючим на даний час стандарртом, транзисторам присвоюються позначення, які складаються з чотирьох елементів:

перший елемент - літера або цифра, що вказують на матеріал, з якого виготовлений транзистор (Г або І  - германій, К або 2 - кремній, А або 3 - арсенід галію);

другий елемент - літера, яка позначає вид транзистора (Т - біполярний, транзистор; П - польовий);

третій елемент - цифри, перша з яких визначає класифікаційний номер транзистора, а дві наступні (від 01 до 99)[2] - порядковий номер розробки в даному класі. Класифікація транзисторів ведеться за двома параметрами:

n граничній потужності , що розсіюється транзистором і яка забезпечує задану надійність при тривалій роботі, та

n  граничній частоті при увімкненні за схемою СБ. Позначення класів наведені в табл.5.1.

                                                                                                            Табл.5.1.

	Малої потужності 0.3 Вт.	Середньої потужності 0.3  - 1.5 Вт.	Великої  потужності 1.5 Вт.
Низькочастотні < 3 МГц	101 - 199	401 - 499	701 - 799
Середньочастотні = 3-30 МГц	201 - 299	501 - 599	801 - 899
Високочастотні > 30 МГц	301 - 399	601 - 699	901 - 999

Четвертий елемент - літера, яка вказує різновид серед даного типу транзисторів. Вони можуть відрізнятися, скажімо, значеннями параметра  , або будь-яких інших параметрів.

Так, наприклад, ГТ605А розшифровується так: германійовий транзистор, середньої потужності, високочастотний, номер розробки 05, різновид А.  Або КТ315А - кремнійовий, малої потужності, високочастотний, розробки 15 різновид А.

Контрольні питання до розділу

 "Частотні властивості біполярного транзистора"•

І, Чому в транзисторі зміни струму колектора відстають у часі по відношенню до змін струму емітера?

2. Чому в моменти різкої зміни струму емітера спостерігаються сильні сплески величини струму бази?

3. Яким способом можна прискорити рух неосновних носіїв у базі від емітера до колектора?

4. Що таке гранична частота транзистора, увімкненого за схемою СБ? Як вона позначається?

5. Яким є  зв’язок між граничною частотою  та товщиною бази?

6. При якому увімкненні транзистор може успішно працювати до більш високих частот - за схемою СЕ чи за схемою СБ?

7. Який зміст має максимальна частота генерації ?

6. Який фізичний зміст має опір  у еквівалентній схемі Джіаколетто?

9. Який елемент у схемі Джіаколетто моделює ефект Ерлі?

10.Як залежать крутість та опір  від постійної складової струму колектора?                                        

11. Чім відрізняється крутість прохідної характеристики  від крутості, яка фігурує у схемі Джіоколетто? Котра з них більша ?

12. Чи залежить величина від режиму транзистора (граничну частоту вважати

       незмінною) ?

ІЗ. Розшифруйте позначення транзисторів ГТ404Д, КТ340В, КТ8І6Б, КП307Ж.

14. Яке позначення мав би германійовий біполярний транзистор з граничною частотою 8 МГц   та граничною потужністю розсіювання 150 мВт?

Задачі до розділу

1.Знайдіть середній час дифузії електронів через базу германійового -транзистора.      Товщина бази 6 мкм, коефіцієнт дифузії електронів у германії 50 см² с^{-1 .}

2. Обчисліть  граничну частоту  транзистора, увімкненого за схемою СЕ. Середній час дифузії неосновних носіїв через базу 0.1 нс, коефіцієнт  = 0,97 .

3. Чому дорівнюватиме коефіцієнт на частоті Гц, якщо =3 МГц, а ?

4. Визначте граничну частоту транзистора , якщо , а = 30 МГц.

5. Визначте елементи еквівалентної схеми Джіаколетто за такими даними: 1500 Ом;

 = 50;  = 5.10^-4 См; = 2 МГц;  = 1 мА.

---

[1] Оскільки аналізується робота транзистора в області високих частот, то тут і далі під величинами струмів і напруг слід розуміти їх змінні складові, точніше, - їх комплексні амплітуди.

[2] Інколи у великих серіях буває по три або навіть і по чотири цифри, наприклад, КТ3107Е