Этюд 7.

Компьютерная вычислительная математика, о которой было рассказано в шести предыдущих этюдах книги, уже давно была «беременна» символьной математикой[1]. В самых ранних версиях Mathcad можно было ввести функцию пользователя и тут же посмотреть на графике, как выглядит не только она сама, но и ее производная (это было сделано в примере на рис. 2.3) или первообразная. Допустимо численными методами получить функцию корней уравнения и проанализировать влияние на нее различных параметров (см. рис. 2.6). За параболой, к примеру, всегда можно узреть икс в квадрате и сделать соответствующие выводы о свойствах анализируемой функции. Можно мысленно экстраполировать какой-либо график в правый край оси ординат и оценить, чему равен предел соответствующей функции при x, стремящемся к плюс бесконечности. Чем это не математический анализ? Но все это были и есть в каком-то смысле виртуальные функции, производные, интегралы, корни, накрепко привязанные к вычислительным методам и унаследовавшие их погрешности и неповоротливость. Так, в примере на рис. 2.3 график функции строится мгновенно, а график ее производной – заторможено, так как вычисление значения производной в точке – это довольно сложная и не совсем корректная задача прикладной математики. С появлением четвертой версии Mathcad «роды» состоялись, и мы теперь можем проследить, как растет «ребенок», как развиваются средства символьной математики. В пятой версии Mathcad они были несколько расширены и усовершенствованы: появились операторы вычисления неопределенных интегралов, пределов (включая «правые» и «левые») и производных высших порядков[2]. Кроме того, были улучшены операции работы с суммой и с произведением: стало возможным работать не только с векторами , но и с конечными и бесконечными суммами . В седьмую версию Mathcad был введен оператор символьного преобразования с ключевым словом g g ® и стало возможным применять средства символьной математики к выражениям, содержащим функции пользователя (см. рис. 2.1) и к несложным программам. В восьмой версии Mathcad внешних изменений инструментов символьной математики нет. Но существенно переработан сам механизм символьных преобразований: Mathcad стал правильно выполнять те операции, где он раньше (седьмая версия) делал ошибки или вообще пасовал. Однако некоторые Mathcad-документы с символьными преобразованиями, сделанными в седьмой версии, при переносе их в восьмой Mathcad перестают работать. Вообще говоря, символьная математика «баба» довольно капризная: часто не знаешь, «на какой козе к ней подъехать». Наш заключительный, седьмой этюд книги будет посвящен не только описанию самих средств символьной математики Mathcad, но и приемам «езды» на этой самой «козе».

Инструменты символьной математики пакета Mathcad условно делятся на три группы:

· команды символьной математики меню Symbolic;

· операторы символьных преобразований g ® и g g ®;

· оптимизация численных расчетов через символьные преобразования (режим Optimize).

Рассмотрим их по порядку.

7.1. Команды символьных преобразований

На рис. 7.1 даны примеры выполнения некоторых команд символьной математики из меню Symbolic.

Рис. 7.1. Команды символьных преобразований

Семь комментариев к примерам на рис. 7.1:

1. При символьном вычислении неопределенного интеграла (пункт 1 на рис. 7.1) и при интегрировании выражения константы опускаются (полагаются равными нулю). Отсюда такой «парадокс»: пользователь взял производную синуса в квадрате (см. рис. 7.2), а от полученного выражения ¾ первообразную. По идее должен вернуться прежний синус в квадрате, но мы получаем косинус в квадрате да еще и с минусом. Удивляться здесь можно, только если забыть тригонометрическую форму записи теоремы Пифагора (sin(x)²+cos(x)²=1) и тот факт, что при интегрировании константа принимается равной нулю.

Рис. 7.2. Примеры трех основных команд символьной математики

2. Некоторые команды символьной математики требуют, чтобы перед их выполнением курсором была отмечена переменная, к которой данная команда адресуется (см. верхний предел интеграла в пункте 2 на рис. 7.1 и аргумент синуса на рис. 7.2). В меню Mathcad 7 и 8 Pro[3] в отличие от более ранних версий пакета такие пять команд (Solve – решить относительно переменной, Substitute – заменить переменную, Differentiate – дифференцировать по переменной, Integrate – интегрировать по переменной, Expand to Series – разложить в ряд и Convert to Partial Fraction – преобразовать в элементарные дроби) объединены в подменю Variable[4]. Человек привык, что x – это переменная, k – константа. Если человеку предложить найти корень уравнения a x=b, то он сразу выдаст ответ (x=b/a) без дополнительных вопросов. Mathcad таких условностей (умолчаний) не признает и требует указания переменной дифференцирования, интегрирования и т.д. В остальных случаях достаточно, чтобы все выражение было выделено курсором, как это было сделано с интегралом и дифференциалом пункта 1.1 на рис. 7.1. Можно выделить только часть выражения и применить нужную команду (например, Simplify – упростить) только к ней: было x×x+x×x, получили x²+ x×x, а не 2×x², если перед упрощением курсором была охвачена не вся сумма, а только первое слагаемое[5]. Если правильного выделения нет, то соответствующая позиция меню Symbolic недоступна и, как это принято, прописана не черным, а серым цветом, призывающим пользователя исправить оплошность. Более опасный случай – это неверное выделение которое тем не менее, не блокирует команды меню. Так, в конце рис. 7.2 не было сделано должного упрощения из-за того, что курсор не охватил всего исходного выражения, а просто был помещен на синусе.

3. Если команда пункта 2 (решение уравнений) адресуется не к уравнению, а к выражению, то по умолчанию считается, что оно приравнено к нулю. Если решений более одного, то они выводятся в виде вектора. Решаться могут не только уравнения, но и неравенства. На рис. 7.3 показано, как с помощью команды Solve решается неравенство, которое мы уже пытались решить графически на рис. 6.25, иллюстрируя работу оператора on error.

Рис. 7.3. Аналитическое решение неравенства

4. Команда пункта 1.2 на рис. 7.1 (вывод числового значения выражения с плавающей десятичной точкой[6]) введена в Mathcad по двум причинам. Во-первых, она позволяет делать расчеты с точностью до 4000 знаков – см. диалоговое окно Float Point Evaluation. Три точки в конце команды Float Point… (они есть и в команде Expand to Series… – разложить в ряд) означают, что перед ее выполнением последует уточняющий вопрос. В нашем случае – это точность, с которой отмеченное выражение должно быть вычислено. Обычный (не аналитический, а вычислительный) оператор Mathcad «e=» выводит основание натурального логарифма с не более чем пятнадцатью знаками в мантиссе. В пункте же 1.2 на рис. 7.1 число e вычислено с 20 знаками. Во-вторых, символьная математика пакета Mathcad оперирует некоторыми функциями, которых в самом пакете Mathcad либо нет, либо они там есть, но называются по-другому[7]. Вывести значения таких функций (на рис. 7.1 это интегральный синус Si и интегральный косинус Ci) можно через команду пункта 1.2. Объясняется это тем, что символьная математика – это не развитие пакета Mathcad, а приобретение фирмы MathSoft у фирмы Waterloo Maple ¾ у разработчика пакета символьной математики Maple V (см. раздел 7.4[8]). Отсюда некоторые нестыковки. В пакете Maple V в вычислениях возможны 64 000 (студенческая версия) и 500 000 знаков (профессиональная версия) в мантиссе[9].

5. Нередко при символьных преобразованиях из-за того, что используется чужая разработка (см. выше), ответ получается настолько не вмещающимся в рамки Mathcad (ни по форме – см. Si и Ci, ни по содержанию – число знаков), что он (ответ) не выводится на экран, а по разрешению пользователя заносится в буфер обмена Clipboard (см. пункт 1.2 на рис. 7.1, где вычислялось число p с 4000 знаками). Что с ним делать дальше, пользователь решает сам. Ответ можно перенести в среду Maple V и там «разделать», а можно попытаться вручную доработать в среде Mathcad, уточнив в help’е или в справочнике по высшей математике, что такое интегральный синус Si, интегральный косинус Ci и другие специальные функции. Нестыковки символьной математики объясняются еще и тем, что в сам Mathcad встроено много функций, которых либо нет в среде Maple V, либо они там есть, но называются или работают по-другому. Пример – функция Maximize (Minimize). В среде Mathcad она возвращает координаты максимума (минимума) функции пользователя (см. этюды 2 и 3), а в среде Maple V – само значение максимума (минимума – см. рис. 7.26 и 7.28).

6. В пункте 3 на рис. 7.1 при операции замены переменной на новое выражение нужно в преобразуемом выражении курсором выделить заменяемую переменную (здесь это x). Новое выражение acos(a-2×p) предварительно заносится в буфер обмена командой Copy из меню Edit. В меню Edit можно увидеть сходную команду Replace..., но она проводит замену без учета правил математики (умножение главнее сложения, группирование выражений скобками и др.) и годится только для комментариев или для глобальной (по всем формулам) замены одного имени переменной (функции) на другое. Полезно, например, в конце работы над задачей заменить «ленивые» переменные (t, s, v) на «звучащие» (Time, Расстояние, Объем[10]). «Символьная» замена позволяет не только проверять правильность решения уравнения (это было сделано в пункте 3 по отношению к пункту 2), но решать многие задачи подстановкой и заменой. В пункте 3 на рис. 7.1 заменой переменной x на выражение acos(a-2×p) мы проверили правильность найденного в пункте 2 корня уравнения: после подстановки (замены) исходное интегральное уравнение превратилось в тождество 2×p=2×p, что и требовалось доказать.

7. Многие команды символьных преобразований обратимы. Так, транспонировать («кантовать») матрицу (эта команда хранится в подменю Matrix – см. рис. 7.1) можно любое число раз: положить ее на «бок», а затем поставить «на попа» – M=(M^T)^T. Операция, обратная интегрированию, – дифференцирование и т.д. Не боги горшки обжигают и не боги создают символьную математику (см. название данного этюда), поэтому, осуществив то или иное действие, полезно провести обратную операцию (см. пункт 1.1 на рис. 7.1 и рис. 7.2). Вероятность того, что одна и та же ошибка заложена и в прямом, и в обратном алгоритме (методе), очень низка. Тут кроется одно из принципиальных отличий символьной (аналитической) математики от математики вычислительной, где операция «туда-сюда-туда-сюда...» часто приводит к накоплению ошибки. В символьной же математике этого не может быть потому, что не может быть никогда. Но если ошибка все-таки проскользнет, то по последствиям она превзойдет все ошибки математики вычислительной (переход количества в качество и наоборот, если вспомнить вузовский курс диалектического материализма[11]). Но это и хорошо ¾ допущенная ошибка «кричит» о себе. Прибегая к услугам вычислительной математики, мы, как правило, довольствуемся приблизительным решением. Приблизительное символьное решение – это нонсенс: «Какой у него номер телефона?» – «Не помню». – «Ну, приблизительно?» Исключения из правила – разложение в ряд с конечным числом членов, который замыкается невязкой O(xⁿ)[12]:

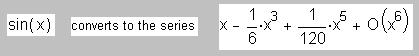
Техника аналитических преобразований с помощью команд меню Symbolic довольно проста:

· пишется или откуда-то копируется исходное выражение (см. пункт 1.1 на рис. 7.1), уравнение (пункт 2) или неравенство (рис. 7.3) – делай раз;

· в выражении (уравнении, неравенстве) курсором отмечается переменная (фрагмент или вся конструкция) ¾ делай два;

· отдается нужная команда из меню Symbolic – делай три.

По умолчанию ответ (упрощенное или преобразованное выражение, корень, число, ряд и т.д.) появляется под исходным выражением, проталкивая вниз то, что было там записано ранее – см. опцию Vertically, inserting lines (вертикально, вставляя строки) в диалоговом окне Evaluation Style (стиль преобразований) на рис. 7.1. По такой схеме на рис. 7.1 сделано самое первое символьное преобразование ¾ взятие неопределенного интеграла от натурального логарифма. Команда[13] Evaluation Style… (последняя в меню Symbolic), вызывает одноименное вышеназванное диалоговое окно, позволяющее отойти от умолчаний в таких направлениях:

· ответ можно получить ниже, но без ввода дополнительных строк (опция Vertically, without inserting lines);

· ответ можно получить правее исходного выражения (опция Horizontally);

· ответ может быть предварен комментарием (флажок Show Comments – см. операцию взятия производной в пункте 1.1 на рис. 7.1; комментарий системы пользователь может дополнить, сделать, например, его перевод с английского);

· ответ может быть записан вместо исходного выражения (опциональный флажок Evaluation in Place).

Троица команд Упростить, Дифференцировать по переменной и Интегрировать по переменной (найти функцию, дифференциал которой – исходная функция) составляет ядро символьной математики Mathcad. Для многих студентов и инженеров этими командами (операциями) ограничивается сам математический анализ.

Из команд меню Symbolic заслуживают особого внимания преобразования Лапласа. Автор неравнодушен к математике[14], но любовь к некоторым ее разделам приходила с годами и с трудом. Но к операционному исчислению (в его основе лежат эти самые преобразования Лапласа) любовь пришла, можно сказать, с первого взгляда – сразу после того, как преподаватель у доски показал фокус: «накрыл» выражение шляпой преобразования Лапласа и поднял ее... Без этого раздела математики невозможно представить такие научные дисциплины, как «Теория автоматического управления», «Основы теории цепей»[15] и др. С помощью обычных двух линеек (простейшая механическая аналоговая вычислительная машина (см. раздел 7.5), где аналог числа – расстояние) можно складывать и вычитать. Если числа нужно перемножить (поделить), то у линеек шкалы делают логарифмическими, что позволяет умножение (деление) свести к сложению (вычитанию) – ведь логарифм произведения равен сумме логарифмов сомножителей. Так устроена обычная (арифметическая) логарифмическая линейка. Преобразования Лапласа можно назвать алгебраической логарифмической линейкой. Они позволяют дифференцирование (интегрирование) заменить умножением (делением). Вот как выглядит «кругосветное путешествие» синуса (поиск производной у функции, а затем поиск первообразной у производной функции) с помощью преобразований Лапласа в среде Mathcad (рис. 7.4).

Рис. 7.4. Преобразования Лапласа в среде Mathcad

Магеллан во время своего турне потерял календарные сутки. При интегрировании командой меню Symbolic (см. рис. 7.1 и рис. 7.2) константы также теряются. Кругосветное «путешествие» синуса через преобразования Лапласа (см. рис. 7.4) обошлось без потерь – исходный синус вернулся с константой С за счет того, что в промежуточных выкладках «вылезла» функция Dirac, равная бесконечности при нулевом аргументе и нулю в остальных случаях.

Команды символьных преобразований, собранные в меню Symbolic в среде Mathcad 7 и 8, Pro стали лишними[16]. Эти команды стали неким рудиментом более ранних версий (как функция until), подарком тем, кто к ним привык. Их стоит рассматривать как некие инструменты работы с базой данных по аналитическим преобразованиям (производные, интегралы, ряды и т.д.), которые в виде таблиц помещаются на первых страницах справочников по высшей математике. С одной стороны, к командам символьной математики стоит прибегать и в случае довольно простых преобразований, подобных таким, которые зафиксированы на рис. 7.1 и рис. 7.2. Дело в том, что при ручной работе неизбежны опечатки[17]. С другой стороны, элементарные преобразования следует делать самому. Это, во-первых, тренирует голову, а во-вторых... Все мы сейчас пользуемся телефонами с памятью и, звоня родным или знакомым, просто нажимаем на кнопку с именем человека вместо того, чтобы набрать номер. Все это хорошо, но если приходится звонить близким с чужого телефона, то зачастую вспомнить номер бывает трудно, а в записной книжке его, естественно, нет. Один студент автора не смог вспомнить производную от e^x и побежал к компьютеру уточнить, чему она равна...

Рис. 7.5. Решение дифференциального уравнения средствами символьной математики Mathcad

На рис. 7.5 командами символьной математики решается дифференциальное уравнение. Вернее, ищется одно из его решений. Полное решение можно увидеть на рис. 7.5. В конце рис. 7.5 читатель видит новый символ «®»[18], который переводит повествование от команд к операторам символьных преобразований.

7.2. Операторы символьных преобразований

Эти операторы позволяют работать со средствами символьной математики уже не в ручном (см. рис. 7.1-7.5), а в автоматическом режиме. В среде Mathcad знак «=» означает числовой, а знак «®» – символьный вывод значения переменной, функции или выражения, записанного от этого знака. В ряде случаев оператор «®» более удобен, чем оператор «=». Автор не смог удержаться и уже в этюде 1 на рис. 1.4 и на рис. 1.14 вел расчеты через оператор «®».

На рис. 7.6 даны типовые примеры работы оператора «®»: взятие производных разных порядков (пункт 1), вычисление неопределенного интеграла[19] и определенного интеграла с бесконечным верхним пределом (пункт 2), вычисление суммы (пункт 3) и произведения (пункт 4), взятия пределов.

Рис. 7.6. Примеры работы оператора символьных преобразований

В ряде случаев оператор «®» возвращает комментарий (см. в пункте 5 ответ “undefined” – «неопределенно») при попытке вычисления предела функции 1/x без указания стороны, с которой мы приближаемся к нулю. В других случаях оператор «®» возвращает само исходное выражение (производную n-го порядка) или выражение с конструкцией, не встроенной в Mathcad, – интегральный синус, например:

Сейчас мы возьмем задачи из первых этюдов книги и по-новому их решим с помощью оператора «®».

На рис. 7.7 приведено аналитическое решение задачи о купце и сукне из этюда 1.

Рис. 7.7. Аналитическое решение задачи о купце и сукне

Команда Solve из меню Symbolic годится только для решения одиночных уравнений и неравенств. Ее «численные» аналоги – функции root и polyroots. Для решения систем уравнений и неравенств предназначена функция Find, которая способна возвращать как численный, так и аналитический результат в зависимости от того, что за ней проставлено – символ «=» или «®». Во втором случае функция Find не требует первого приближения. На рис. 7.7 функция вернула Find аналитическое решение системы двух линейных алгебраических уравнений, которое было скопировано и в которое были подставлены конкретные значения переменных.

На рис. 7.8 приведен аналитический поиск минимума функции Розенброка (численное решение задачи показано на рис. 3.4), в которой константы 100 и 1 заменены на переменные a и b.

Рис. 7.8. Аналитический поиск минимума функции Розенброка

Здесь через функцию Find аналитически решается система уравнений (пункт 1), собранная из частных производных функции Розенброка по x и y, приравненных к нулю.

Показано, что значение переменной a не меняет положение точки минимума – оно существенно влияет на процесс численного решения задачи, удлиняя овраг, на дне которого находится минимум. В этом можно убедиться, вернувшись к рис. 3.4 и изменив в функции Розенброка сотню, к примеру, на единицу.

Далее на рис. 7.8 в пункте 2 продолжены «деривации» этюда 3: сделаны попытки проверки на «аналитичность» двух других встроенных Mathcad-функций, также предназначенных для решения оптимизационных задач. Функция Minimize отказалась работать (пункт 2.1), а функция MinErr выдала непонятно что (пункт 2.1). Пункт 2 на рис. 7.8 – это по сути протокол экспериментов над программной средой, которые в принципе не возбраняются, но плодами которых нужно пользоваться очень осторожно.

На рис. 7.9 приведено аналитическое решение задачи о балке из этюда 1 (см. рис. 1.12, 1.15 и 1.16).

Рис. 7.9. Аналитическое решение задачи о равновесии балки

Три выражения, которые вернула функция Find (пункт 1), мы использовали в этюде 1 для иллюстрации графических возможностей Mathcad (см. рис. 1.17-1.19 и 1.21-1.25).

В пункте 2 на рис. 7.9 показан и второй способ решения системы уравнений через оператор символьного преобразования с ключевым словом (здесь ключевое слово solve – решить). Прежде чем описывать эту новую конструкцию, отметим, что в символьных преобразованиях Mathcad перестают работать встроенные единицы измерения: если оба плеча балки измеряются в метрах, то выдается правильный ответ, однако если второе плечо выражено в дюймах – ответа нет.

На рис. 7.10 приводятся образцы заготовок, которые возникают на экране дисплея в отмеченном курсором месте после нажатия клавиш панелей инструментов Evaluation и Symbolic:

Рис. 7.10. Панели работы с операторами символьных преобразований

Сам оператор символьных преобразований вводится в Mathcad-документ нажатием кнопки g ® на панели Evaluation или Symbolic. После этого на экране дисплея появляется такая заготовка: g g ®. Первый операнд данного оператора – это какая-либо алгебраическая конструкция (выражение, неравенство, уравнение и др.), а второй – ключевое слово, задающее направление символьного преобразования[20]: упростить, решить, факторизировать, вычислить коэффициенты полинома и т.д. Оператор символьного преобразования с ключевым словом существенно богаче по своим возможностям команд меню Symbolic. Поэтому, как было отмечено выше, это меню фактически лишнее. Кроме того, оператор символьного преобразования сразу выдает новый ответ, если в исходном выражении что-то поменяли. Здесь не нужно стирать старый ответ, как это требуется при обращении к командам меню Symbolic.

Само ключевое слово оператора g g ® (второй его операнд) может иметь новый ключ, определяющий детали символьного преобразования. Только две команды (Simplify – Упростить[21] и Complex – представить в комплексном виде) не имеют дополнительных ключей. Чтобы в них не запутаться, лучше не выводить на экран заготовку оператора g g ®, а поступать по-другому: записать или откуда-то скопировать исходное выражение (a+b×x=0, например) и нажать на кнопку с названием соответствующего преобразования (solve, например). После этого на экране появится уже не заготовка оператора решения уравнения, а его, так сказать, полуфабрикат: a+b×x=0 solve, g ®. В черный квадратик достаточно вставить имя переменной, по которой решается уравнение, чтобы получить ответ: -b/a. Здесь можно оперировать не только переменной, но и новым выражением – x - 1, например:

Особо хочется отметить оператор разложения на множители g factor, g ®. Если его применить не к алгебраическому выражению, а к числу натурального ряда, убрав при этом его ключ (g factor ®), то он будет называться Разложить на простые множители. Простые числа – это такие числа, которые делятся без остатка либо сами на себя (результат – единица), либо на единицу (результат – само простое число). Простые числа (2[22] – единственное четное простое число, 3, 5, 7, 11, 13, 17, 19, 23 и т.д. до бесконечности) – простые и по названию, и по определению, но за ними стоит много проблем теоретического и практического плана, одна из которых такая...

Сэм, Билл и Джон договорились... Нет, не сразиться на дуэли (см. этюд 6), а обмениваться друг с другом шифрованными сообщениями по таким правилам:

· каждый i-й участник придумывает свой шифрующий (ША_i) и дешифрующий (ДША_i) алгоритмы;

· шифрующие алгоритмы открыты, они известны всем участникам;

· свои дешифрующие алгоритмы каждый участник держит в секрете;

· если i-й участник захочет послать шифрованное сообщение j-му участнику, то он использует ША_j (он, как мы договорились, известен всем);

· j-й участник, получив сообщение от i-го участника, использует ДША_j, который, как мы знаем, известен только j-му участнику;

· i-й участник может послать j-му участнику шифрованное сообщение с электронной подписью[23]; для этого i-й участник, посылая сообщение j-му участнику, использует цепочку шифров ДША_i-ША_j. Получив сообщение, j-й участник читает его так: ДША_j-ША_i, восстанавливая исходный текст. При этом j-й участник будет знать, что только i-й участник мог послать такой дважды зашифрованный текст, так как при шифровании был использован ДША_i, известный только i-му участнику.

Все это выглядит просто и красиво. Проблема заключается в разработке шифрующих и дешифрующих алгоритмов. Поступим для начала так. Пусть все участники переводят свое сообщение из текста в число N (“АББА” – 01020201, например). Затем по шифрующему алгоритму Сэм возводит число в квадрат, Билл – в куб, а Джон – в четвертую степень (ША₁:=N²; ША₂:=N³; ША₃:=N⁴). Дешифрующие алгоритмы (их участники должны держать в секрете) сводятся к извлечению квадратного корня, кубического корня и корня четвертой степени соответственно и в переводе полученного числа в текст. Но такая тайна будет тайной Полишинеля, так как криптоаналитику ничего не стоит, просмотрев несколько сообщений, раскрыть не только шифрующий алгоритм (а из этого никто особой тайны не делает), но и дешифрующий. Проблема создания надежных функций-ловушек (функций, обратный алгоритм которых невозможно раскрыть, сколько ни анализируй прямой алгоритм), до сих пор полностью не решена. В криптографии пока довольствуются функциями-ловушками с «потайной кнопкой», расположение которой известно только владельцу шифра. Прятать такую кнопку можно с помощью простых чисел.

Дело в том, что сгенерировать простое число можно довольно быстро. Тем более (тем быстрее) на компьютере. Но если два довольно больших простых числа перемножить и попросить компьютер по произведению найти исходные сомножители, то эта задача окажется неразрешимой, вернее, для ее решения потребуются «миллионы лет работы самого современного компьютера»[24].

Итак, участники «шифровальной дуэли» разрабатывают шифрующие алгоритмы, используя простые числа так, что посторонний, анализируя послания, может узнать только произведение (составное число). Проблема раскрытия дешифрующего алгоритма сводится к нахождению сомножителей – к разложению числа на простые множители.

Рис. 7.11. Разложение чисел на простые множители

На рис. 7.11 даны примеры работы оператора n factor ®. Если исходное число n простое, то система Mathcad довольно быстро (секунды, минуты) доказывает это и выдает один сомножитель – само исходное простое число. Короткие составные числа раскладываются на простые сомножители также за приемлемое время. Но если составное число удлинить, то Mathcad «задумывается» намертво. Не «зависает», а именно задумывается. Автор оставлял включенную машину на выходные: вместо курсора-стрелки появлялся курсор – докторская четырехуголка, что свидетельствовало о работе символьного процессора. В понедельник ответа не было, а после нажатия клавиши Esc, вызывающего диалоговое окно прерывания вычислительного процесса, и щелчку по кнопке OK работоспособность Mathcad восстанавливалась:

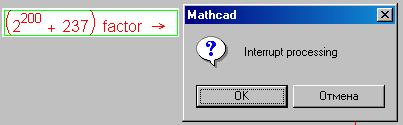
Простые числа на рис. 7.11 – это не просто простые числа, взятые наугад, а числа из различных литературных источников, где они отмечались как самые большие простые числа, известные человеку на определенных этапах развития математической науки и техники счета. Числа вида 2ⁿ-1 называют числами Мерсенна (http://www.mersenne.org). Они могут быть простыми лишь в том случае, если n – простое число (условие необходимое, но недостаточное – число 2⁶⁷-1 составное, хотя число 67 простое). До сих пор не доказано, имеется ли конечное или бесконечное число простых чисел Мерсенна[25]. То же можно сказать и в отношении простых чисел, состоящих только из единиц.

Особо хочется отметить число 2⁵²¹-1. На рис. 7.11 показано, что это число Мерсенна – простое. Но в книге Мартина Гарднера (о ней ниже), сказано, что в 1982 году суперкомпьютер[26] «Крей» разложил его на три простых множителя за 32 часа работы. Где здесь ошибка? Либо Mathcad неправильно факторизирует числа, либо в книге Гарднера прошла опечатка (очепятка). Второе вероятнее, так как в книге отмечено, что это 69-значное число, тогда как на самом деле оно имеет больше знаков. Предлагаем читателю самому разобраться в этом вопросе. Автору тут важно поднять проблему и наметить пути ее решения с помощью Mathcad.

Для проверки чисел на простоту используют так называемую малую теорему Ферма[27] (см. пункт 2 на рис. 7.11). Если p – простое число, а число a – случайное, меньшее, чем p, то функция Ferma возвращает единицу. Если р – составное число, то функция Ferma возвращает число, большее единицы. И большая и малая теоремы Ферма пока считаются не доказанными, но если кандидат на простое число несколько раз выдерживает тест Ферма[28], то его считают «условно» простым и используют в шифровальном деле.

Я только что изложил главу «Надежные шрифты» из книги Мартина Гарднера «От мозаик Пенроуза к надежным шрифтам» (М.: Мир, 1993). После ее прочтения у меня возникло такое чувство, что либо я сам что-то недопонимаю, либо и меня и Гарднера кто-то искусно водит за нос, отвлекая от раскрытия настоящих алгоритмов шифрования.

Вот отрывок из этой книги.

«Объясняя, как работает их (шифровальная. – здесь и далее примечания автора) система, авторы из МТИ (Массачусетский технологический институт) выбрали в качестве исходного текста парафраз ремарки из «Юлия Цезаря» Шекспира (акт I, сцена 2): "ITS ALL GREEK ТО ME" («Для меня все это сущая тарабарщина» – мы говорим «китайская грамота», англичане же при этом вспоминают греков).

Прежде всего, этот текст преобразуется в одно большое число с помощью стандартного ключа: А=01, В=02, ..., Z=26 (00 – пробел между словами). Получается число 09201900011212000718050511002015001305.

Полученное число шифруется путем возведения его в s-ю степень по модулю некоторого составного числа r. Составное число r получается как произведение двух случайно выбранных простых чисел p и q, каждое из которых не менее чем 40-значно. Число s должно быть взаимно простым с числом p-1 и q-1. Числа s и r общедоступны: они используются в шифрующем алгоритме. Операция шифрования осуществляется весьма эффективно даже при очень больших значениях r; на практике она требует менее одной секунды компьютерного времени.

Два простых множителя числа r хранятся в памяти компьютера, поскольку они используются в секретном обратном алгоритме. Обратный алгоритм, используемый при дешифровке, состоит в возведении числа-шифротекста в другую степень t и в нахождении остатка от деления полученного числа на r, то есть в приведении по модулю r. Как и в предыдущем случае, на это уходит менее секунды машинного времени. Но показатель t может вычислить только тот, кто знает p и q ¾ два простых числа, которые хранятся в секрете.

Если исходный текст слишком велик для того, чтобы с ним можно было обращаться как с одним числом, то его следует разбить на блоки и каждый блок рассматривать как отдельное число. Я не буду вдаваться здесь в дальнейшие подробности. Они носят несколько технический характер и ясно изложены в отчете МТИ.

Для шифрования текста ITS ALL GREEK TO ME группа из МТИ выбрала s=9007 и r=114381625757888867669235779976146612010218296721242362562561842935706935245733897830597123563958705058989075147599290026879543541.

Число r есть произведение 64-значного простого числа p и 65-значного простого числа q, каждое из которых выбрано случайным образом. Шифрующий алгоритм заменяет число, соответствующее исходному тексту (09201...), следующим числом-шифротекстом: 199935131497805100452 31712274026064742320401705839146310370371740625971608948 927504399209626725826750128935544613538 23769748026.

Желая поощрить тех читателей журнала «Scientific American[29]», которые хотели бы испробовать свои силы на поприще криптоанализа, группа из МТИ зашифровала с помощью того же общедоступного алгоритма другой текст. Шифротекст вы видите на рис. 92 (см. книгу Гарднера). Его оригинал представляет собой предложение на английском языке. Сначала оригинальный текст был превращен в число с помощью стандартного метода, который был объяснен выше, полученное число возведено в 9007-ю степень (по модулю r) с помощью остроумного метода, изложенного в отчете. Тому, кто первым расшифрует текст, группа из МТИ обещала выплатить премию в 100 долларов.

Для доказательства того, что шифротекст действительно исходит от группы из МТИ, к нему была добавлена следующая подпись: 16717861150380844246015271389168398245436901032358311217835038446929062655448792237114490509578608 655662496577974840004057020373.

Подпись зашифрована с помощью секретного обратного шифрующего алгоритма. Так как читатель не располагает своим общедоступным шифрующим алгоритмом, вторая шифрующая операция была опущена. Каждый читатель, имеющий доступ к компьютеру и алгоритмам, опубликованным в отчете МТИ, может легко прочитать подпись с помощью общедоступных шифрующих алгоритмов группы МТИ, то есть возвести приведенное выше число в 9007-ю степень и перейти к остатку от деления на r. Проделав эти операции, читатель получит число 06091819200019151222051800230914190015140500082114041805040004151212011819. Пользуясь стандартным ключом, читатель расшифровывает это число как FIRST SOLVER WINS ONE HUNDRED DOLLARS («первый, кто расшифрует текст, получит сто долларов»). Этот подписанный шифротекст мог быть получен только от группы из МТИ, так как обратный алгоритм, которым был зашифрован исходный текст, известен только членам этой группы.»

На этом заканчивается отрывок из книги Гарднера. Он сначала писался Гарднером по-английски, затем набирался в типографии, потом переводился на русский язык, опять набирался в типографии, затем сканировался автором для вставки в данную книгу. При такой технологии ошибки в числах текста очень вероятны. Тут вспоминается старая карикатура. Человек с перевязанными руками и ногами лежит на больничной койке, а диктор по телевизору, поставленному в палате, говорит: «Приносим извинения! В нашу вчерашнюю передачу «Делай с нами, делай как мы, делай лучше нас!» вкралась ошибка». Римейк карикатуры. «Пациент «палаты № 6» в книге по компьютерной математике читает приписку: «В наше предыдущее издание вкралась ошибка».

Автор перемножил в среде Mathcad[30] два простых числа и поместил произведение в пункте 3 на рис. 7.1. Кто первым определит, что за простые числа были перемножены (найдет потайную кнопку шифра), получит приз, название которого также зашифровано: «Кмапвсптор к мвуепа»[31].

Оператор символьного преобразования с ключевым словом можно считать зачатком нового языка программирования, ориентированного не на вычислительный, а на аналитический процесс. Но интеграция символьной математики в среду Mathcad еще слаба и требует обилия ручной работы, без которой не составить даже функции пользователя из преобразованного выражения.

Один из коллег автора пришел в полный восторг, увидев действие пары expand – series. Ему (а он преподаватель математики в институте) по долгу службы приходится составлять вопросы для вступительных экзаменов. Ключевые слова expand – series позволяют как из рога изобилия сыпать вопросами с заголовком «Упростить», заранее имея правильный ответ. Несколько охладила этот восторг мысль о том, что абитуриенты пронесут на экзамен ноутбук[32] и ключевыми словами factor и simplify все эти примеры «разъяснят». Правда, на экзамене, как и в самом учебном процессе, требуется не столько ответ, сколько промежуточные выкладки... К проблеме щита и меча во взаимоотношениях ученика и учителя мы вернемся чуть позже, рассматривая место пакета Mathcad и ему подобных в процессе преподавания не только чисто технических дисциплин, но и самой высшей математики.

В среде Mathcad 8 можно вести цепочку символьных преобразований, показывая или не показывая промежуточные выкладки, которые иногда бывают настолько громоздкими, что их не то что рассмотреть – стереть с экрана бывает затруднительно.

Рис. 7.12. Решение задачи о балке средствами символьной математики

На рис. 7.12 показано, как оператор solve с решает нашу старую задачу о раскрое коробки (коробок) максимальной вместимости: берется квадратная заготовка, по углам которой вырезаются маленькие квадратики. Полученная таким образом крестовина складывается в коробку (см. схему на рис. 2.4 в этюде 2). Найти параметры раскроя, дающие максимальный объем коробки. В этюде 2 мы развили эту известную школьную задачу, отметив, что из обрезков можно делать новые коробки, которых в принципе может быть бесконечное множество.

Комментарии к рис. 7.12:

· В пунктах 1 (одна коробка) символьные преобразования ведутся «цугом» с выводом промежуточных аналитических выражений. Такая цепочка операторов получается следующим образом: записывается оператор дифференцирования (см. пункт 1) и нажимается кнопка оператора символьного преобразования «®» в панели Simbolic:

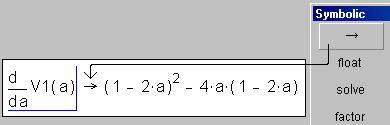
Далее ответ (производная от функции V1) охватывается курсором и нажимается кнопка Simplify в той же панели инструментов:

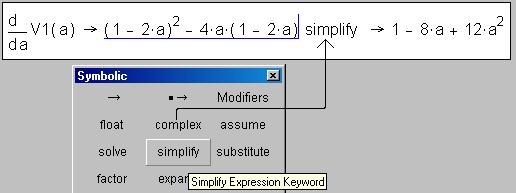
Затем к упрощенной производной прикладывается оператор решения уравнения (solve, a), возвращающий два корня, первый из которых (1/6) – ответ по задаче о коробке.

· В пункте 2.1 (бесконечное число коробок с постоянной пропорцией раскроя a) символьные преобразования также ведутся «цугом». Одно из неудобств такой технологии в том, что промежуточные результаты выстраиваются по горизонтали и из-за этого их неудобно рассматривать на экране дисплея и распечатывать на бумаге принтера. На рис. 7.12 (а это, как читатель знает, «заморозка» экрана дисплея, доработанная в среде графического редактора) промежуточные выражения выстроены по вертикали, где стрелки показывают последовательность преобразований. Аналитический ответ (а численного здесь получить нельзя из-за того, что суммируется бесконечный ряд) – это вектор уже с четырьмя элементами, последний из которых (0.1736…) – решение задачи. Здесь дополнительно задействован оператор float, n, возвращающий число с плавающей точкой с n[33] знаками[34].

· В пункте 2.2 операторы, решающие задачу о бесконечном числе коробок, выстроены не «цугом», а «парой», если так можно выразиться. При этом промежуточные результаты не показываются, так как они очень громоздки, и ничего не дают ни уму ни сердцу. Обычно пользователь комбинирует «упряжку» символьных преобразований, получая какое-то подобие «шестерни», когда лошади идут парами цугом.

· В решении двухмерной оптимизационной задачи о пяти коробках (пункт 3 – два шага раскроя) выведены и аналитические и численные ответы (их четыре; правильный – второй).

· В решении трехмерной оптимизационной задачи о двадцати одной коробке (1+4+16 –пункт 4) выведены только численные ответы (их двенадцать; правильный – восьмой сверху). Честно говоря, задача о любом числе коробок сводится к одномерной оптимизации последовательными решениями: пропорция последнего раскроя равна 1/6; зная это, можно одномерной оптимизацией найти раскрой первого шага из двух при пяти коробках и т.д. Здесь просматривается рекурсия, к которой мы еще вернемся в конце этюда.

Из рис. 7.12 видно, что символьный процессор пакета Mathcad выдает много лишних ответов. Из-за этого не только увеличивается объем Mathcad-документа, но и неизбежны сбои, когда символьная математика отказывается выполнять простейшие, на взгляд человека, операции или выполняет их не так как надо. В связи с этим в среду Mathcad введены операторы и ключи, позволяющие игнорировать (по-английски to assume) некоторые направления преобразований. На рис. 7.13 даны примеры таких игнорирований. Во-первых, пустой с точки зрения вычислительной математики оператор присваивания x:=x (пример 1 на рис. 7.13) лишает переменную x (или какую-то другую) ее численного значения. В примере 2 упрощается квадратный корень из икса в квадрате. Результат получается разным в зависимости от типа переменной x.

Рис. 7.13 Игнорирования при символьных преобразованиях

По умолчанию тип всех переменных, участвующих в символьных преобразованиях, – комплексное число. Отсюда и соответствующее «упрощение» квадратного корня из квадрата – scgn(x)×x. Можно игнорировать отрицательные значения переменной (assume, x³0) и получить на самом деле упрощенный ответ – x. Ключ assume=real заставляет рассматривать все переменные в качестве вещественных (реальных). При этом можно оговорить диапазон изменения значений вещественных переменных – ключ assume=RealRange(0,¥). Ключ trig заставляет в тригонометрических преобразованиях учитывать тождество sin(x)²+cos(x)²=1.

7.3. Оптимизация численных расчетов

Третий инструмент символьной математики пакета Mathcad, который позволяет с определенной долей условности назвать его системой искусственного интеллекта[35], связан с оптимизацией численных расчетов. Вспомним исторический анекдот, приписываемый королю математиков – Гауссу (см. сноску 17).

...До конца урока оставалось десять минут, и учитель решил отдохнуть – он занял учеников, среди которых был и маленький Гаусс, рутинной работой – подсчетом суммы чисел натурального ряда от 1 до 100. Но через мгновение Гаусс поднял руку и выдал ответ – 5050. Он не стал складывать единицу с двойкой, полученную тройку с тройкой и т.д., а... перемножил сумму первого и последнего членов ряда на 50. Ведь сумма второго и предпоследнего членов также равна 101, как и сумма третьего и предпредпоследнего, а таких пар в сотне ровно пятьдесят.

Посмотрим, как среда Mathcad следует примеру не только маленького, но и взрослого Гаусса.

Рис. 7.14. Задача маленького Гаусса

Пакет Mathcad с выключенным режимом оптимизации (умолчание), столкнувшись с суммированием, начнет по примеру нормальных (талант – это аномалия) одноклассников Гаусса прибавлять к единице двойку и т.д.: 1+2+3+4+5+...+100. В среде Mathcad мы тоже можем написать такое длинное выражение, но проще воспользоваться оператором суммирования – см. рис. 7.14. Если в примере на рис. 7.14 увеличить значение n до миллиона, например, то время счета станет неприемлемо долгим. Если это не суммирование, а интегрирование (в руководстве пользователя Mathcad приведен пример с тройным интегралом), то это сути дела не меняет: пакет Mathcad будет по-прежнему что-то там долго и упорно суммировать[36], опираясь на соответствующий численный метод (прямоугольников, трапеций, парабол и т.д.[37]). Такие расчеты можно и нужно оптимизировать. В конце рис. 7.14 получена простая формула, которой можно заменить сумму членов натурального ряда: (n²+n)/2. Если включить режим оптимизации (переключателем Optimize в меню Math –см. рис. 7.14), то пакет Mathcad будет пытаться во всех выражениях искать упрощающие формулы и работать уже с ними, а не с исходными выражениями. Это будет глобальная оптимизация. Возможна и «точечная», локальная оптимизация, когда упрощающая формула ищется только для отдельных выражений. Для этого правой кнопкой мыши вызывается локальное меню с командами, применимыми к математическому выражению, а через него вызывается диалоговое окно свойств выражения Properties[38]. В этом окне у позиции Enable Optimization (возможность оптимизации) ставится флажок[39]. Включенный тем или иным способом режим оптимизации суммы (произведения, интеграла, дифференциала – всего, что можно заменить более простой формулой, – см. первые страницы справочников по высшей математике) заставляет систему Mathcad вспомнить о лаврах Гаусса и отказаться от лобовой атаки. Если более оптимальное решение найдено (его поиск отображается мерцанием на экране докторской четырехуголки – признак того, что работает символьная математика), то правее выражения появляется красная шестиугольная звезда[40]. Свершилось чудо – машина стала считать не только быстрее, но и умнее. Пользователь может просмотреть не только численный результат, но и аналитическое выражение, упростившее расчеты (заменившее собой сумму). Оно заносится в специальный буфер, отображаемый на дисплее командой Show Popup в локальном меню или щелчком по красной звездочке.

Программисты могут здесь вспомнить оптимизирующие компиляторы, вмешивающиеся не только в кодирование алгоритма, но и в упрощение формул. Ввел программист строку S := (A * A - B * B) / (A - B), нажал Enter, а на экране – S := A + B.

Оптимизация в задаче маленького Гаусса – это стрельба из пушки по воробьям: отрезок суммируемого ряда надо значительно увеличить, «чтобы почувствовать разницу» во времени счета. При каком значении n такая оптимизация оправдана – это новая оптимизационная задача: оптимизация, так сказать, в квадрате. Оставим ее для студенческих лабораторных работ, а сами стрельнем из пушки не по воробьям, а по... двум зайцам и покажем, что в ряде случаев оптимизация не только ускоряет расчеты, но и повышает их точность. Скажем осторожнее – влияет на точность. И не только количественно, но и качественно – за счет исправления методологических ошибок (промахов) численных методов и их конкретных оптимизаций в среде Mathcad.

Упоминавшийся пример оптимизации интеграла из документации к пакету Mathcad тривиален – ясно, что криволинейная трапеция (сам интеграл) и набор маленьких вписанных прямоугольников (приближение к интегралу) никогда не сравняются по площади. А вот более сложный пример (рис. 7.15), показывающий двойственность процесса оптимизации.

Рис. 7.15. Загадка оптимизации

Какой ответ (лобовой – 25 007 600 или хитрый – 24 999 750) правильный, сказать трудно. Автор не стал отыскивать оптимизационный алгоритм или расчетную формулу, а составил BASIC-программу и использовал ее в качестве «третейского судьи» (см. рис. 7.16). Ее запуск выдал на дисплей второе число (24 999 750), что свидетельствует в пользу «второго зайца» – оптимизация не только ускоряет расчеты, но и делает их более точными даже при работе с целыми числами. Математики, к которым автор обратился как к высшим судьям, подтвердили правильность расчетной формулы и дефектность прямого счета. Дело, по-видимому, в том, что на языке C (а на нем писался и Mathcad и Maple V) очень просто запутаться в циклах с пересекающимися параметрами, если при этом нужно оптимизировать еще и саму программу.

Dim n As Integer

Dim i As Integer

Dim j As Integer

Dim k As Integer

Dim S As Long

n = 100

S = 0

For i = 1 To n

For j = 1 To n - i

For k = 1 To n

S = S + k

Next

Print “Ответ:”; S

Запуск программы

Ответ: 24 997 500

Рис. 7.16. BASIC-программа – «третейский судья»

Но и с BASIC-программой на рис. 7.16 не все так просто – в цикле с параметром j может оказаться и оказывается так, что n-i (конечное значение параметра цикла) становится меньше единицы (первое значение параметра цикла). В этом случае заголовок цикла должен оканчиваться оператором Step - 1. В нашей же программе шаг изменения параметра по умолчанию всегда равен плюс единице (см. также описание цикла for в этюде 6).

Рассказывая о преподавателе математики, который пришел в восторг от новых ключевых слов expand и series, до предела упрощающих составление вопросов для экзаменов, автор высказал опасение, что абитуриент пронесет на экзамен ноутбук и без труда все решит. Именно «пронесет», а не принесет. За стилистическими различиями скрывается большая проблема, связанная с принятием или непринятием компьютерной математики в преподавании школьных и вузовских дисциплин.

После того как автор стал использовать пакет Mathcad в курсе «Оптимизация химико-технологических процессов», ход занятий кардинально изменился. Раньше разбору сути научно-технической проблемы удавалось отводить не более 20% учебного времени, а остальные аудиторные часы «уходили в гудок» – тратились на разъяснение методов оптимизации и способов их реализации на языках BASIC, C, fortran. Пакет Mathcad и ему подобные перевернули эту ненормальную пропорцию: появилась возможность быстро и элегантно (у английского слова smart есть и другой перевод – «элегантно») решать поставленные задачи без кодирования алгоритма, а в естественном их представлении не только численно, но и аналитически. К программированию приходится прибегать лишь в крайних случаях, когда стандартных средств не хватает. А среда Mathcad позволяет дополнять свой арсенал новыми функциями, программируя их (см. этюд 6). Но эта работа – удел избранных. Основная масса студентов никогда серьезно программировать не будет. Учить их программированию для заполнения графика учебной нагрузки можно, но эффект от этого будет минимальным, а удовольствия никакого. Как игра на скрипке требует особого музыкального слуха, так и написание серьезных программ немыслимо без особого программистского чутья («слуха»), которым обладают далеко не все.

Сейчас в среде преподавателей живо обсуждается вопрос о месте компьютера в процессе изучения высшей математики. Реакций на появление описываемых в книге инструментальных средств две: (а) «держать и не пущать» и (б) кардинально менять методику и содержание учебных курсов. Калькуляторы ликвидировали устный счет как род занятий по арифметике. Автор, учась в начальной школе, должен был через три секунды дать правильный ответ на вопрос: «Сколько будет, если помножить 89 на 76?» Теперешним школьникам, вооруженным калькуляторами, такие вопросы могут только в страшном сне присниться. Здесь впору и сожалеть: устный счет – прекрасная гимнастика для ума. Недаром старый Болконский мучил княжну Марью алгеброй, а самые знаменитые биржевые аферисты – прекрасные математики (вспомним финансовую пирамиду из этюда 5). Есть опасение (или надежда – кому как), что средства символьной математики ликвидируют такие формы практических занятий, как поиск пределов, интегралов, разложение функции в ряд, дифференцирование и др. А это львиная доля содержания семинаров по математике.

Проблема же компьютера на вступительном экзамене по математике снимается довольно просто: если абитуриент с его помощью решит все задачи, то ему впору не пятерку ставить, а диплом выдавать.

На самом деле реакций на появление средств символьной математики не две, а три. Третья реакция определяется не отношением преподавателей к этому ноу-хау, а отношением общества к самим преподавателям. При нынешнем уровне оплаты учителям впору спасибо говорить лишь за то, что они входят в аудиторию и ведут занятия по накатанному пути и на довольно высоком уровне. О кардинальной переделке методики и содержания учебных курсов не может быть и речи. Для этого к занятиям нужно основательно готовиться[41], а времени нет: чтобы прокормить семью, надо халтурить (образчик такой «халтуры» перед глазами читателя). Да и сама символьная математика пока не так совершенна, чтобы можно было все бросить и ухватиться за нее. Тот же Гаусс в гробу перевернулся бы, если б увидел, как пакет Mathcad оптимизировал его несколько измененную школьную задачу. Оказывается, что перестановка слагаемых местами меняет сумму.

Рис. 7.17. Парадокс режима оптимизации

Подобная неприятность случается и при использовании оптимизирующих компиляторов, о которых мы уже упоминали и работать с которыми нужно очень осторожно. Автор когда-то долго бился над одной программой, пока не понял, что оптимизирующий компилятор упорно выносит за рамки цикла системную переменную, считая ее константой. Ошибки вычислительной математики, как правило, понятны и простительны, ошибки же символьной математики иллюстрируются пословицей: заставь дурака богу молиться – он и лоб расшибет. Фокус рис. 7.17 в том, что там решается квадратное уравнение, у которого, как известно, два корня. В практических расчетах отрицательный корень часто отбрасывается. Его принимают за пришельца из потустороннего мира (отрицательная масса, концентрация, абсолютная температура и т.д.). Символьная математика, желая угодить пользователю, подсовывает ему один корень, но не тот, какой надо. Оба корня (100 и -101) найдены на рис. 7.17.

В Руководстве пользователя Mathcad запрещается в суммах давать верхнему пределу значение меньше, чем нижнему. В этом, наверное, заключается ключ к разгадке проблемы на рис. 7.17. Программа же на рис. 7.16 имеет циклы с положительным единичным шагом параметра, что не вполне соответствует суммам на рис. 7.15 (см. описание цикла с параметром в этюде 6).

Но шутки, тем более грубые, в сторону. Реакция «держать и не пущать» вполне обоснована. Опыт западных университетов показывает опасность подмены традиционных занятий изучением математических пакетов[42]. В процессе решения огромная роль отводится постановке учебной задачи и интерпретации результата. Освоение машинной математики может создать иллюзию освоения самой математики: студент, выполнив кучу команд и получив на дисплее массу чисел, формул и графиков, не знает, что с ними делать дальше, и не понимает, где кроется настоящее решение. Из-за этого многие преподаватели вполне обоснованно считают, что включение в уроки математики компьютера равносильно... дооборудованию спортивного тренажера гидроусилителями[43]. Другое дело старшие курсы, где математический аппарат применяется для решения конкретных научно-технических задач.

В седьмой версии Mathcad символьная математика проникла и в программирование – см. рис. 7.18.

Рис. 7.18. Символьная математика и программирование

Символьная математика пока плохо стыкуется с программами Mathcad. Стоит программы на рис. 7.18[44] слегка усложнить, как тут же появляются сообщения об ошибке. Особенно несовместимы с символьной математикой операторы if, otherwise, break, continue и return (острые углы, которые не терпит природа). В программирование Mathcad проникли пока только зачатки символьной математики из пакета. Подождем новой версии Mathcad, а сейчас обратим свои взоры к Maple V.

7.4. От Mathcad к Maple

Один из разделов лингвистики, называемый сравнительным языкознанием, позволяет выводить общие закономерности, присущие различным языкам. На сравнительном языкознании, как правило, основывается изучение иностранных языков: одно дело учить английскому немца, а другое – китайца. Примерно такой же подход наблюдается и в освоении программных сред: одно дело приступить к работе с Maple, имея опыт общения только с традиционными языками программирования, а другое – набив руку на Mathcad. В этом – ключ к пониманию следующего раздела книги. Рассказывая о математической программе Maple V[45], автор сравнивает ее с программой Mathcad и с языком BASIC.

Мы уже упоминали о том, что символьная математика Mathcad взята из пакета Maple. Из-за этого символьное решение задачи в среде Mathcad нередко приводит к результату, понятному только пользователю Maple, идеологию и структуру которого автор попытался описать ниже.

7.4.1. Идеология

В начале было Слово...

Начало Евангелия от Иоанна утверждает примат Слова. А вот как начинается «евангелие» от фирмы Waterloo Maple, Inc., описание пакета Maple: «Maple V is a Symbolic Computation System or Computer Algebra System». Этим декларируется, что в Maple главенствует Символ (выражение, уравнение, функция и т.д.), а не Число. Разработчики сразу оговаривают, что Maple – это математика, а не вычислительная математика. За прилагательными в названиях научных дисциплин нередко таится некая ущербность[46], которая хорошо иллюстрируется гипотетическим диалогом на Шаболовке: «Папа, кто построил эту башню?» – «Инженер Шухов». – «Это как наша мама – инженер?» – «Нет, сынок, наша мама – старший инженер». Пакет Maple с самого начала был задумал и реализован сугубо как инструмент символьных преобразований. В среде Maple пользователи оперируют исключительно символами, «опускаются» до числа крайне редко и, можно сказать, крайне неохотно – когда, например, не удается аналитически решить дифференциальное уравнение и приходится использовать численные методы.

Пакет же Mathcad изначально создавался для численного решения математических задач (1988 г.). Инструменты символьной математики были интегрированы в Mathcad совсем недавно (1994 г. – четвертая версия). За свою десятилетнюю историю пакет Mathcad как бы повторил многовековой путь развития самой математики, в которой долгое время господствовало число (арифметика, геометрия) и только на пороге новой истории появился символ (алгебра, математический анализ). Но многие пользователи Mathcad по-прежнему считают символьную математику рекламной штучкой, выполняющей лишь вспомогательные и демонстрационные функции.

Считается, что Maple – это университетская компьютерная математика, а Mathcad – математика технических вузов. И не только потому, что первый пакет опирается на символ, а второй – на число. Решение математических задач в среде Maple требует как умения оперировать той или иной встроенной функцией, так и основательного знания методов решения, в нее заложенных: во многих встроенных функциях Maple фигурирует аргумент, задающий метод решения. Что такое корень уравнения и какая функция (процедура) может его отыскать – знает каждый, кто использует математические пакеты, но какие методы при этом применяются – для многих тайна за семью печатями. Одну из таких «тайн» мы пытались раскрыть на рис. 3.1, анализируя функцию root.

7.4.2. Интерфейс

В столицах женщины получают, может быть, лучшее образование; но навык света скоро сглаживает характер и делает души столь же однообразными, как и головные уборы.

А.С.Пушкин. Барышня-крестьянка

Пушкин говорит о том, что без индивидуальности не может быть ни настоящей красоты, ни настоящего величия. Индивидуальность того или иного пакета проявляется не только в наборе математических инструментов (душа), но и в интерфейсе (внешность). Если говорить о наиболее распространенных версиях Mathcad и Maple (существуют их версии для разных платформ – DOS, Windows, Mac[47], UNIX...), то, перефразируя Пушкина, можно сказать, что в среде Windows прикладные программы получают, может быть, лучшие возможности для связи с другими приложениями и периферией; но идеология Windows скоро сглаживает программы и делает их столь же однообразными, как их интерфейс.

«Душа» Maple ведет свою родословную от fortran[48], вернее от богатых математических библиотек, наработанных за долгую жизнь этого языка. Первые элементы компьютерной алгебры появились именно в нем: ввел, например, программист строку a = (x**2 - y **2) / (x - y), а компилироваться будет уже другая, упрощенная – a = x + y. В свою очередь, интерфейс Maple – это не что иное, как режим немедленного выполнения операторов языка BASIC.

Все слышали о трех революциях в программировании: структурной (ее отголоски звучали в этюде 6, когда мы рассуждали о метке в программе), объектно-ориентированной и визуальной. Но мало кто помнит, что настоящую, и в каком-то смысле единственную революцию в программировании совершил BASIC-интерпретатор. В «дореволюционное» время нужно было сначала писать программу, затем компилировать ее в машинные коды и только потом – получить результат. Пользователь не видел промежуточных результатов и не мог вовремя вмешаться в вычислительный процесс. Из-за этого основная масса распечаток шла прямиком в мусорную корзину. С языком BASIC пришла новая технология. Открыв любой старый учебник по этому языку, можно прочитать: «Если в начале вводимой строки стоит номер, то эта строка становится строкой создаваемой (редактируемой) программы. Если номера у строки нет, то операторы строки немедленно выполняются после нажатия клавиши Enter». На рис. 7.19 приведен протокол немедленного выполнения операторов в среде языка GW-BASIC, входящего в состав MS-DOS 3.x. Пример простой, но за ним стоит многое.

a = 3: print a: REM Исходная величина

b = a^(1/77): print b

1.01437

c = TAN(b)^99: print c

2.605988E+20

d = ATN(c^(1/99)): print d

1.01437

e = d^77: print using"#.##############";e

3.00000071525574

Рис. 7.19. «Путешествие» тройки в среде языка BASIC

Этот протокол показывает, что происходит манипуляция исходной тройкой сначала прямыми (степень, тангенс), а потом обратными (корень, арктангенс) действиями, в связи с чем в переменную e возвращается уже нетройка (тройка с хвостиком).

В среде Mathcad (рис. 7.20) текстовый режим ввода выражений заменен на графический. Кроме того, знак присвоения «=» заменен на знак «:=», а оператор print реализуется через Mathcad-оператор «=». Но это сути дела не меняет: тройку постигла та же печальная участь, что и на рис. 7.19.

Рис. 7.20. «Путешествие» тройки в среде Mathcad

Пакет Maple – это, грубо говоря, BASIC-интерпретатор, к которому «прицепили» более 2500 встроенных функций, решающих разнообразные математические задачи: поиск корней уравнений и систем, построение графиков, оптимизация, линейная алгебра, интегральные преобразования, линейное программирование, статистика, тензорный анализ, анализ функций комплексных переменных, теория графов, комбинаторика и многое другое.

Основной (а для многих пользователей – единственный) режим работы Maple – это режим немедленного выполнения команд строки. Как и в среде BASIC, они вводятся в виде текста, а двоеточие служит разделителем операторов. На экране дисплея в среде Maple по умолчанию строки ввода прописаны красным цветом, графический отклик системы – синим, а комментарии пользователя – черным. У языка GW-BASIC цветового выделения не было (впервые этот прием был использован в языке Quick Pascal, а сейчас расцвечивают почти все программы[49]). Готовность интерпретатора «слушать» очередную фразу пользователя (который постепенно переставал быть программистом) отмечалась восклицанием Ok, аналогичным слову «прием» у радистов. А вот как выглядит «кругосветное путешествие» тройки в среде Maple (рис 7.21).

Рис. 7.21 «Путешествие» тройки в среде Maple

Глядя на рис. 7.19-7.21, можно утверждать, что Maple – это BASIC, в котором поменяли идеологию (структуру хранения и обработки данных); а Mathcad – это BASIC, в котором изменили интерфейс. Короче говоря, Maple – это BASIC сегодня. (Сравнение, конечно, еще то! Вспомним другое: «Сталин – это Ленин сегодня». Автору в свое время набили голову всякой идеологической мурой, которая всплывает из глубин памяти в самые неожиданные моменты. Вот еще одно идейно выдержанное определение: «Mathcad – это материалистическое направление развития языка BASIC, а Maple – идеалистическое».)

Интерфейс Maple ориентирован на тех пользователей, которые уже набили руку на программировании в средах традиционных языков с вводом сложнейших формул в текстовом режиме. Для таких людей ввод квадратного корня и других математических операций с помощью нажатия соответствующих кнопок на панелях инструментов (технология Mathcad – см. рис. 1.3 в этюде 1) – чистой воды профанация. Редактирование в графическом режиме ранее введенной формулы для них часто становится вообще неразрешимой задачей. Те же, кто с пеленок вкусил легкость и удобство ввода формул в их естественной «многоэтажной» математической нотации Mathcad, морщат нос от всяких там sqrt, int, diff (корень, интеграл, дифференциал – технология Maple) и т.д. Именно на них ориентирован интерфейс Mathcad, и в этом, наверное, одна из причин его популярности. В пятой версии Maple появилась возможность ввода текстовых заготовок функций через нажатие соответствующих кнопок – см. рис. 7.21.

7.4.3. Структура данных

Не спеши выполнять приказ: очень вероятно, что его отменят.

Армейский и деловой фольклор

Вышеприведенная трилингва BASIC-Mathcad-Maple не только поясняет особенности интерфейса при работе в этих средах, но затрагивает и более глубокие пласты. Ахиллесова пята численных методов – это погрешность расчетов. Очень часто даже самая мизерная ошибка вычислений искажает расчет и может свести на нет ценность результата. Символьная компьютерная математика протаскивает через чащу преобразований исходную величину в ее первозданном виде: на рис. 7.21 во всех многоэтажных формулах, как в скорлупе, сидит исходная тройка. «Не спеши выполнять приказ: очень вероятно, что его отменят» – это бюрократическое правило порождает не только волокиту, но и амортизирует неразумные распоряжения начальства и просьбы посетителей. Maple не спешит переводить число в традиционную форму (в вещественное число с плавающей запятой, например) и не попадает в ловушку, подобную той, какая проиллюстрирована на рис. 7.19 и 7.20 (исчезновение тройки). Функция evalf в среде Maple может возвратить значение переменной длиной до 500 000 знаков. Но тройку из выражения, хранимого в переменной е, абсолютно безошибочно и сверхбыстро может извлечь («разбить скорлупу») первая и в каком-то в смысле главная функция символьной математики – simplify (упростить). Одним словом: не спеши вычислять – очень вероятно, что это не понадобится[50].

Протоколы на рис. 7.19 и 7.20 – это, в сущности, реализация на компьютере детской игры в испорченный телефон. Игрок а задумывает слово и шепчет его с небольшими искажениями игроку b, тот – игроку c и т.д. Слово по цепочке переходит к последнему игроку, который громко называет то, что услышал от соседа. Игрок a называет исходное слово, и тут раздается хохот – спутник любой игры. Но искажения чисел компьютером вызывают не смех, а слезы. Переход от числа к символу при решении задач на компьютере по значимости можно сравнить с переходом от аналогового к цифровому способу записи звука и изображения.

Символьная форма хранения числа позволяет решить не только проблему точности, но и проблему экономии памяти компьютера: например, корень из трех, записанный в символьном виде (Ö3), хранит 1,73... (до бесконечности). Программисту при работе с Maple уже не надо ломать голову над выбором типа переменных (одинарная, двойная и прочая точность). Если говорить о сверхточности, обеспечиваемой «длинными» типами переменных, не следует забывать, что природа не любит не только острых углов, но и избыточности. Если решение «разваливается», это может свидетельствовать не только о дефекте в вычислительной процедуре, но и о неправильной исходной модели. Вот еще один диалог, но уже не на Шаболовке, а в музее. Экскурсовод: «Этому экспонату один миллиард и двадцать лет». – Посетитель: «Откуда такая точность?!» – Экскурсовод: «Когда я поступил сюда на работу, мне сказали, что этому экспонату миллиард лет, а с тех пор прошло еще двадцать». Подобной излишней педантичностью страдает и автор: на многих рисунках книги в расчетах оператором «=» выводятся все 15 знаков числа, хотя там достаточно трех-четырех.

Переменные в среде Maple могут хранить (естественно, в символьном виде) все что угодно: константу, выражение, функцию, равенство, неравенство, график, геометрический образ и т.д. Сами же переменные группируются в последовательности (sequence), массивы (array), списки (list), множества (set) и таблицы (table). Элементом массива может быть список, элементом списка – массив и т.д. Комбинируя структуры и создавая новые, пользователь способен моделировать довольно сложные математические абстракции, ограничивая себя лишь своей фантазией и объемом памяти компьютера. По знаменитой формуле Вирта: программа – это алгоритм плюс структура данных. Говоря о Maple, можно сказать, что протокол решения задачи – это умело спроектированная структура символьных данных, процеженных сквозь сито функций и команд. В Maple встроен fortran-подобный язык, позволяющий реализовывать сложные алгоритмы, но к программированию прибегают в особых случаях – Maple и Mathcad задумывались как средства программирования без программирования (в те времена слова «работа на компьютере» и «программирование» были почти синонимами). К программированию и в среде Maple, и в среде Mathcad прибегают в тех случаях, когда для решения задач не хватает встроенных средств (см. этюд 6).

Существует ошибочный взгляд на компьютерную символьную математику как на вычислительную математику без погрешностей и ошибок. Пример, приведенный на рис. 7.22, опровергает это мнение[51].

Рис. 7.22. «Роковое путешествие» тройки в среде Maple

Протокол на рис. 7.22 почти полностью повторяет протокол на рис. 7.21, только в формулах число 77 заменили на 2, а число 99 – на 3. Задачу упростили, но тем не менее исходная тройка в ней безвозвратно потеряна. Вместо нее вылезло комплексное число, на тройку совсем не похожее. Ошибки вычислительной математики искажают числа слегка (см. рис. 7.19 и 7.20), ошибки символьной математики почти всегда бывают фатальны. Но чаще приходится говорить не об ошибках, а о взаимном недопонимании пользователя и программы. Фокус рис. 7.22 состоит в том, что арктангенс – это не совсем обратная тангенсу функция, а квадратный корень из числа – это не совсем то же, что число в степени одна вторая. Еще раз повторяем, что без хорошего знания математики к Maple лучше не обращаться.

Одно время, когда персональные компьютеры были у нас новинкой, за работающим у дисплея человеком пытались наблюдать психологи. Наблюдать и делать выводы, которые, как правило, были двух сортов: психолог либо формулировал всем известную истину либо психолог изрекал явную глупость. Умный психолог выбирал третий вариант – он молчал. Что-то подобное можно отметить, анализируя работу символьной математики. Несложно придумать пример (см. рис. 7.22), на котором она «сломается» и выдаст «неправильный» результат (Mathcad и BASIC задачу на рис. 7.22 решают «правильно»). Более-менее простые аналитические преобразования выполняются вручную, и компьютер ничего нового здесь не открывает. Обычная (увы) реакция компьютера на сложные задачи – молчание (см. рис. 7.24, где показана попытка аналитического решения дифференциальных уравнений).

7.4.4. Примеры

Лучше один раз увидеть, чем сто раз услышать.

Русская пословица

Нет ничего практичней хорошей теории и нет ничего численней хорошего аналитического решения задачи. Пример, приведенный на рис. 7.23, особо поражает тех, кто занимается или когда-то занимался составлением программ решения дифференциальных уравнений. В среде Maple эта задача решается буквально в два счета: делай раз – запись уравнения (рис. 7.23), делай два – его решение в аналитическом виде.

Рис. 7.23. Решение дифференциального уравнения в среде Maple

Инструменты символьной математики Mathcad (см. рис. 7.5) позволяют найти за раз только одно из решений (без констант) дифференциального уравнения, записанного на рис. 7.23. Пользователю при этом придется поработать головой и руками, преобразуя исходное уравнение в интегральное, копируя промежуточные выкладки и т.д. Поэтому знание математики нелишне и при работе с Mathcad.

Возвращаясь к теме интерфейса Maple, отметим, что документ Maple может быть структурирован пользователем: если щелкнуть по кнопке, расположенной левее названия параграфа, то соответствующая область захлопнется и останутся только название параграфа и кнопка – но уже не с минусом, а с плюсом внутри. Это очень удобно при работе с объемными документами. Такая технология заложена во многих Windows-приложених, например в текстовом редакторе Word. В последних версиях Maple и Mathcad допустимы гипертекстовые ссылки.

Как понимает читатель (вернее, знает из курса высшей математики), далеко не всякое дифференциальное уравнение имеет аналитическое решение, описываемое комбинацией известных математических функций и операторов, да и не всякое существующее аналитическое решение удается найти. Кроме того, очень часто аналитическое решение бывает настолько громоздким, что от него приходится отказываться, особенно если нужно найти решение в точке (задача Коши). На рис. 7.24 решается известная задача о развитии эпидемии из этюда 5. Напомним суть задачи. В городе с 22 тыс. жителей появляются 50 инфекционных больных, что вызывает эпидемию. Предположим, что прирост больных за день пропорционален (с коэффициентом Pr[52]) произведению числа здоровых (еще не переболевших и не приобретших иммунитет) на число больных. Спрашивается, как развивается эпидемия, то есть как изо дня в день (переменная t) меняется число больных (функция x) и число здоровых (y). Проблема сводится к решению задачи Коши для системы двух обыкновенных дифференциальных уравнений.

Рис. 7.24. Задача об эпидемии в среде Maple

Maple решил систему аналитически. Но что с этим «решением» делать дальше?!

На рис. 7.25 представлен протокол решения в среде Maple задачи о равновесии балки (решение этой задачи в среде Mathcad дано на рис. 1.15 и рис. 1.16 в этюде 1) – поиск реакций опор x, y и Р, которое сводится к решению системы трех алгебраических уравнений, описывающих баланс сил и их моментов. Задача решается полностью на аналитическом уровне и заканчивается формированием функции y, по которой строится трехмерный график.

Рис. 7.25. Задача о балке в среде Maple

7.4.5. Графика

По одежке встречают, по уму провожают.

Русская пословица

«Одежка» всех математических пакетов – это их графика. Красочные объемные конструкции, подобные той, которая завершает решение задачи о балке (см. рис. 7.25), помещают в рекламных буклетах, на обложках описаний и на коробках с дистрибутивами всех математических программ. В среде Mathcad фактически нет графиков функции, а есть только визуализация данных, хранящихся в векторах и матрицах. В среде Maple достаточно иметь только вид функции одной или двух переменных, чтобы строить самые сложные графики (декартов, полярный, с логарифмическими шкалами осей, параметрический) и поверхности (в декартовых, сферических, цилиндрических (см. рис. 7.25), спиральных координатах). Также в среде Maple допустима визуализация данных из векторов и матриц.

Вот еще ряд существенных преимуществ графики Maple по сравнению с графикой Mathcad:

• в среде Mathcad поверхность может строиться только в прямоугольной области существования двух аргументов, а в среде Maple это ограничение снято: границы области существования графика можно задавать и аналитически (пример – рис. 7.27);

• в среде Maple допустимо в одной области документа через функцию display помещать разнотипные графики: комбинировать, например, декартов и полярный график, цилиндр со сферой и т.д., если в этом есть, конечно, какой-то математический смысл. Математический смысл конструкции в пункте 5 на рис. 7.25 отыскать довольно сложно. Тут у нас получилась задача не о балке, а о проектировании вазы необычной формы, которую уместно поставить в офисе фирмы, разрабатывающей или продающей математические пакеты;

• в среде Maple создание и форматирование графиков возможно не только через меню (как в среде Mathcad), но и через параметры (ключи) соответствующих команд. Это позволяет программно управлять графикой: если какая-то кривая выходит за отведенные ей пределы, то она автоматически «краснеет», и т.д.;

• в среде Maple есть специальный тип графики, ориентированный на визуализацию решений задач определенного класса: дифференциальных уравнений, определения области существования аргументов, конформных преобразований, поиска множества корней, линейного программирования (рис. 7.29) и т.д.;

• Maple допускает построение различных геометрических абстракций (линий, фигур, тел) через задание их параметров.

7.4.6. Программирование

А роза упала на лапу Азора

А.Фет

Средства реализации сложных алгоритмов были введены только в версию Mathcad PLUS 6.0 (1995 г. – см. этюд 6). Maple же с самого начала задумывался как язык управления символьными преобразованиями. Его команды, как уже было отмечено ранее, выполняются немедленно после нажатия клавиши Enter. Но ничто не мешает собрать эти команды воедино и сформировать из них новые функции и процедуры, поместить их в тело цикла или альтернативы и т.д.

В описании Maple сказано, что это fortran-подобный язык. Под этим подразумевается, что он не prolog-подобный, не APL-подобный и не lisp-подобный (на языке lisp в 1958 году John McCarthy написал программу поиска производных функций, которая стала «первой ласточкой» компьютерной символьной математики), но скорее BASIC-подобный. И не только из-за возможности непосредственного выполнения операторов, но и из-за своего синтаксиса. Различия – в деталях. Разработчики языка Maple, по-видимому, увлекаются палиндромами – текстами, которые читаются одинаково слева направо и справа налево (см. эпиграф). В языке Maple альтернатива, как и во всех других языках, начинается с ключевого слова IF, а заканчивается новым ключевым словом FI (IF наоборот). Такая же заготовка-палиндром (DO...OD) предусмотрена для тела цикла и т.д. Программисту наконец-то открывается широкая возможность написания программ-палиндромов типа IF A THEN NEHT A FI. Написание стихов-палиндромов относится к области экспериментальной поэзии (В.Хлебников и др.). Язык Maple может быть инструментом экспериментального программирования. Автор одно время был очень увлечен экспериментальным программированием. В его коллекции есть, например, программа численного интегрирования методом прямоугольников, состоящая из прямоугольных блоков. Другая программа рассчитывает числа Фибоначчи: число знаков в каждой ее строке совпадает с числами Фибоначчи. Третья программа ищет минимум функции методом золотого сечения. Она вписана в рамки структурной диаграммы, стороны которой находятся в золотом соотношении.

Язык Maple обладает всеми качествами «настоящего» языка программирования. Так, язык Maple оснащен средствами отладки, чего, к сожалению, нет у языка Mathcad.

Maple состоит из ядра (kernel), написанного на языке С и включающего в себя поддержку основных функций. Из ядра пакета можно вызывать большое количество библиотек (см. на рисунках команду with(название библиотеки), написанных на языке Maple. В Release 4 насчитывается 31 библиотека: combinat, combstruct, DEtools, difforms, Domains, finance, GaussInt, genfunc, geometry, grobner, group, inttrans, liesymm, linalg, logic, LREtools, networks, numapprox, numtheory, orthopoly, padic, plots, plottools, powseries, process, simplex, stats, student, sumtools, tensor и totorder. Такой набор инструментов определяет и высокую цену пакета[53]. Кроме того, он требует защиты – Maple V Release 4 работает только с электронным ключом. Все библиотеки съедают до 24 Мбайт дискового пространства.

Но здесь кроется и одна из главных причин того, что у нас пакет Maple менее популярен, чем Mathcad. Приобретая Maple, пользователь получает своеобразный «подарочный набор», включающий в себя вещи, которые ему никогда не понадобятся. Кроме того, универсальность очень часто (увы!) подразумевает облегченность – нельзя объять необъятное. Автор, к примеру, протестировал библиотеку simplex (решение задач линейного программирования симплекс-методом). С учебными задачами она справляется, но если их слегка усложнить, то ответа можно и не дождаться. Maple явно перегружен. Из-за этого, например, многие одноименные встроенные функции имеют разное содержание и разные аргументы после загрузки разных пакетов.

Разработчики Mathcad «пошли иным путем». Они сделали ставку на электронные учебники и Internet. Нужно пользователю решить дифференциальное уравнение – он либо покупает отдельно соответствующий электронный учебник, который содержит описание задачи и функции, обеспечивающие ее решение, либо через Internet открывает на отдаленном сервере файл с прототипом задачи. Если пользователю Mathcad требуется неординарная графика, то он может воспользоваться пакетом Axum. Одновременно с Maple V Release 4 (лето 1996 года) на рынке появилась новая версия Mathcad под названием StudyWorks. Она стоит около 50 долл., содержит мультимедийный обучающий курс и, главное, как и Mathcad 8 Pro, предоставляет пользователям широкие возможности коллективной работы через Internet. Платой за использование чужих открытых библиотек должна быть разработка и открытие миру своих собственных.

7.4.7. Вывод

Право, какое затруднение – выбор! Если бы один, ну два пакета, а то – четыре. Как хочешь, так и выбирай! И Mathcad недурен (правда, худощав – всего 250 встроенных функций), и Maple неплох, и Mathematica, хоть и толстовата (несколько тысяч встроенных функций, операторов и команд), – тоже видный пакет, да и MatLab не без достоинств. Как тут быть?

Автор пошел по простому пути – он взял монолог Агафьи Тихоновны из гоголевской «Женитьбы» и заменил в нем названия женихов на названия популярных математических пакетов. Агафья Тихоновна, если помните, мечтала о том, чтобы «губы Никанора Ивановича да приставить к носу Ивана Кузьмича, да взять сколько-нибудь развязности, какая у Балтазара Балтазаровича, да, пожалуй, прибавить к этому еще дородности Ивана Павловича...». Пользователь математических пакетов, к счастью, может их интегрировать, решая поставленную задачу. Настоящий раздел книги – это своеобразные смотрины двух современных математических программ – Mathcad и Maple.

Mathcad в каком-то смысле универсальный, но не специализированный пакет. В нем есть и средства решения уравнений и систем (алгебраических и дифференциальных), и средства оптимизации, и научная графика, и символьная математика, и линейная алгебра, и статистика, и многое другое. Однако если пользователю, к примеру, нужно углубиться в символьную математику, то ему лучше работать не с Mathcad, а с Maple. Серьезные задачи линейной алгебры требуют MatLab и т.д. Многие ругают Mathcad, сравнивая его с MatLab или с пакетом Mathematica, забывая при этом, что MatLab и Mathematica стоят почти на порядок дороже Mathcad.

Ниже приводится еще несколько задач, решенных и в среде Mathcad и в среде Maple.

На рис 7.26 показано, как в среде Maple решается задача из этюда 2 о пожарном ведре (см. рис. 2.2).

Рис. 7.26. Задача о пожарном ведре в среде Maple

Вот некоторые отличия в идеологиях Mathcad и Maple:

· Maple-документы должны начинаться с команды restart. Дело в том, что в среде Mathcad действие оператора «:=» распространяется вниз и вправо в текущем документе. В среде же Maple действие оператора присвоения распространяется не только во все стороны документа, но и на другие открытые документы. Команда restart – это своего рода «санитарный кордон», пересекающий действие ранее объявленных переменных, функций, библиотек и т.д.;

· Maple более близок к традиционным языкам программирования из-за текстового режима ввода строк. Все математические кнопки Mathcad в среде Maple имеют буквенную кодировку: квадратный корень – sqrt, интеграл – int, дифференциал – diff и т.д. Нужно также помнить латинскую транскрипцию греческих букв: alpha, beta, gamma и т.д.;

· при построении декартова графика в среде Maple нет необходимости указывать число точек на графике. По умолчанию их 50. Этот принцип перешел в среду Mathcad, но не полностью. Забегая вперед – к рис. 7.27, следует отметить, что в среде Maple до предела упрощена и процедура построения поверхности: достаточно сообщить имя функции двух переменных и диапазон изменения аргументов. Размер сетки (grid) и другие параметры поверхности задаются по умолчанию. В среде Mathcad построение поверхности сопряжено с предварительным заполнением матрицы значениями функции двух переменных. При этом значения аргументов терялись, вместо них появляются эрзац-аргументы – номера строк и столбцов матрицы;

· в среде Maple есть функция maximize, возвращающая максимальное значение (естественно, символьное) анализируемой функции. В среде Mathcad похожее действие производит функция max, возвращающая элемент вектора или матрицы с максимальным значением.

Лобовая атака на три пожарных ведра (рис 7.27) в среде Maple не удалась (численное решение задачи на рис. 2.7).

Рис. 7.27. Задача о трех пожарных ведрах в среде Maple

Минимум функции Розенброка в среде Maple (рис. 7.28) отыскивается без проблем.

Рис. 7.28. Функция Розенброка в среде Maple

В этюде 3 мы решили задачу о краске – задачу линейного программирования. А вот как в среде Maple решается другая подобная задача – об оптимальном плане выпуска стульев.

Суть задачи. Мебельная фабрика может выпускать стулья двух типов – по 8 и 12 тысяч рублей. Под этот заказ выделены материальные и людские ресурсы: 440 погонных метров досок, 65 квадратных метров обивочной ткани и 320 человеко-часов. Известно, сколько досок, ткани и времени идет на изготовление каждого стула:

Стул	Расход досок, м	Расход ткани, м²	Расход времени, чел.-час.
Первый	2	0.5	2
Второй	4	0.25	2.5
Ресурс	440	65	320

Спрашивается, как нужно спланировать производство стульев, чтобы наделать их ценой поболее. Это и отображено в отчете о решении задачи на рис. 7.29.

Данная задача относится к широкому классу задач под названием задачи линейного программирования: необходимо установить план (программу!) выпуска изделий (у нас это стулья), ориентируясь на целевую функцию (общая стоимость стульев) и принимая во внимание ограничения (ресурсы по доскам, ткани и человеко-часам).

Рис. 7.29. Решение задачи о стульях в среде Maple

Для решения задачи линейного программирования в среде Maple подгружается специальная библиотека simplex. При этом появляется предупреждение (Warning) о новом содержании функции maximize. Функция inequal из библиотеки plots позволяет визуализировать решение задачи линейного программирования с двумя переменными: прямые линии отсекают лишнее и оконтуривают область существования решений (затемненная область). Решение задачи находится на одной из вершин полученного многоугольника и отыскивается модернизированной функцией maximize.

В среде Maple функция solve (решить) имеет много модификаций, определяемых префиксом. Просто solve решает алгебраические уравнения и системы, dsolve - дифференциальные и т.д.

В протоколе на рис. 7.30 функция rsolve ищет рекуррентные (r) формулы для поиска чисел Фибоначчи (см. в этюде 6 рис. 6.13 и 6.14).

Рис. 7.30. Maple и числа Фибоначчи

В книге рассматриваются программы, работающие под управлением Windows. Эта операционная система позволяет интегрировать различные прикладные пакеты, а возможность перебрасывать задачу из одной программной среды в другую, избегая их отрицательных качеств и эксплуатируя положительные, – уже путь к успеху. Кроме того, не следует забывать о гибридности решения задач...

7.5. Гибридное решение задачи на компьютере

Два числа можно сложить, переведя их в двоичную систему (разложив на нули и единицы), пропустив через лабиринт логических операций процессора компьютера и сделав обратное преобразование полученной суммы из двоичного в десятичное представление. Так работают электронные цифровые вычислительные машины – ЭЦВМ. С числами можно поступить иначе: взять, например, два переменных сопротивления, соединить их параллельно и подать на них напряжение. Изменяя величину сопротивлений (выставляя два слагаемых - ток, проходящий через сопротивления) и замеряя общий ток, можно найти искомую сумму. Так работают аналоговые вычислительные машины (АВМ) – аналог сложения берется из области физики электричества (закон Ома, закон Кирхгофа и др.). Если нужно решить систему дифференциальных уравнений (а это был «хлеб» аналоговых машин), то в дело шли законы электромагнитной индукции (Максвелл & Co): конденсатор – дифференцирование, катушка – интегрирование и т.д. Кроме электрических были (а где-то еще и есть) механические, гидравлические и даже пневматические аналоговые вычислительные машины.

А вы ноктюрн сыграть смогли бы на флейте водосточных труб?

А вы в DOOM сыграть смогли бы на пневмо-АМВ?

Красивую в своей простоте управляющую механическую АВМ можно видеть в музеях истории техники (в московском Политехническом, например). Она стоит на старых паровых машинах: два металлических шара вращаются на системе рычагов и регулируют подачу пара в цилиндры так, чтобы скорость хода была постоянной при любой нагрузке. Менее изящную, но тем не менее также очень полезную гидравлическую управляющую АВМ можно увидеть не выходя из дома – заглянув в бачок, пардон, унитаза.

Были времена[54], когда АВМ и ЭЦВМ работали на равных, и пользователи (вернее программисты и операторы, пользователей тогда еще и в помине не было) остро ощущали их плюсы и минусы. Стремление к приумножению достоинств и к ликвидации недостатков вызвало к жизни так называемые гибридные машины, решающие вычислительные задачи и аналоговыми и цифровыми средствами. Сигнал, подаваемый на осциллограф (решение дифференциального уравнения на аналоговой части машины), обрабатывался в ее цифровой части: выдавалась таблица решения, велась аппроксимация и т.д. Но бурное развитие ЭЦВМ (в первую очередь резкое снижение их цены) похоронило как аналоговые, так и гибридные машины. Сейчас эта ветвь развития кибернетики практически обрублена. А жаль. Величайшую тайну природы – секрет работы головного мозга – нужно исследовать не по линии цифровых, а по линии аналоговых машин (био-АВМ!). Страшно даже представить, что у нас в голове шевелятся не извилины, а какие-то там нули и единицы.

Сейчас вошли в моду шахматные турниры между машиной и человеком (между ЭЦВМ и био-ABM, грубо говоря). Но все прекрасно понимают, что это событие не шахматной, а рекламной жизни (Intel Inside). Даже турниры гроссмейстеров часто не открывают ничего нового в теории шахмат, а просто сводятся к выявлению шахматиста, сделавшего наименьшее число «зевков». Интересно было бы провести соревнование ЭЦВМ с «гибридной машиной» – с этаким шахматным кентавром – с перворазрядником, работающим в паре с компьютером, который, во-первых, страхует от «зевков», а во-вторых, выдает варианты очередных ходов. Гибрид человека и компьютера – это основа современных систем управления, сбои в которых дорого обходятся человечеству (Чернобыльская катастрофа, например).

Теперь, когда мы говорим «ЭВМ» или просто «компьютер», то имеем в виду только цифровую технику. Но ностальгия по старым добрым временам породила программы, имитирующие работу аналоговых машин на персоналке: пользователь на дисплее соединяет «проводками» изображения конденсаторов и катушек, с помощью реостатов выставляет константы и... решает систему дифференциальных уравнений: на фантомном осциллографе чертится кривая, «вольтметры» замеряют потенциал и т.д.[55] Появление таких виртуальных АВМ связано не только с ностальгией, но и с более глубокими чувствами. Моделируя реальный объект на ЭЦВМ, мы получаем его суррогат – рафинированное изображение, процеженное сквозь сито нулей и единиц. На АВМ живет кусочек реальности. Пушкинский Дон Жуан, увидев «узенькую пятку» Доны Анны, смог дорисовать весь ее облик. Оператор АВМ через кривую на осциллографе не просто видит, а «печенкой чувствует» траекторию полета космического аппарата со всеми возможными отклонениями, связанными не с ошибками вычислительных методов, а с самой природой.

Но вернемся с небес на землю – к теме книги – программному обеспечению компьютеров.

Отмеченное раздвоение в подходах к решению задач наметилось и в программных средствах для цифровой техники. С одной стороны, есть инструментарии численных методов, с другой – возникли и бурно развиваются средства символьной математики.

Гибридность решения задачи в среде Mathcad в полной мере проявляется при включенном режиме Optimize (Оптимизировать – см. раздел 7.3). В этом режиме пакет, столкнувшись с численной задачей (вычисление определенного интеграла, например), не будет сразу вызывать соответствующую процедуру, реализующую метод Ромберга, а постарается найти первообразную подынтегрального выражения и работать уже с ней. Но вот тривиальный пример – определенный интеграл от a до a. Человек и без численных методов и без символьной математики знает, что он равен нулю. А что будет делать машина? Среда Mathcad с выключенным режимом оптимизации также сразу выдаст нуль. А с оптимизацией она будет долго и упорно искать первообразную для подынтегрального выражения... У автора в запасе есть набор примеров подшучивания над Mathcad (см. начало этюда 3), ставящих на место любую сверхумную систему и показывающих, что человек еще долго будет царем природы – как живой, так и неживой.

Механизм аналитических преобразований, введенный в Mathcad, придал его старым «цифровым» встроенным функциям свойство, которое с определенной долей условности можно назвать полиморфизмом[56]. Пример – функция Find. Если за ней поставить знак «=», то будет выведено числовое значение решения системы алгебраических уравнений, а если знак «®», то – аналитическое. Функция Find (как и многие другие встроенные функции Mathcad) несколько странная, и мы это уже отмечали. Все нормальные функции возвращают свое значение в зависимости от своего имени, числа и значений аргументов (принцип инкапсуляции, если опять же оперировать терминами объектно-ориентированного программирования; механизм вложения функций, широко используемый в Mathcad, заставляет вспомнить и о третьем «ките» ООП – о механизме наследования). Так вот, функция Find возвращает свое значение в зависимости от того, что находится около нее до ключевого слова Given.

Работая с Mathcad, под гибридностью следует понимать сочетание аналитических, численных и интуитивных методов решения задачи, что проиллюстрировано примером на рис. 7.31. Решается все та же нами любимая задача об одном пожарном ведре (пункт 1) и о двух пожарных ведрах (пункт 2). При решении задачи формируются две функции пользователя r(a) и h(a) – радиус и высота конуса, размеры которых зависят от параметров раскроя круглой заготовки (см. схему на рис. 2.1). Из этих функций строится выражение для расчета объема ведра, от которого берется производная[57].

Рис. 7.31. Гибридное решение задачи о пожарных ведрах

Далее делается попытка решить полученное уравнение (производную, приравненную к нулю) ¾ найти значение угла вырезки a, при котором объем пожарного ведра будет максимальным (там производная равна нулю). Пакету Mathcad такая работа окажется не по зубам: будет выдано сообщение о том, что ответ настолько «неприличен», что его стыдно показывать, а надо прятать в буфер обмена. Из буфера обмена такой специфической ответ можно перенести в Mathcad-документ текстом (для этого готовится текстовая область – нажимается клавиша «“») или числом. В тексте на макроязыке Maple зафиксирована попытка решения уравнения. Числовое решение позволяет еще раз убедиться в том, что Mathcad обладает зачатками чувства юмора: сообщается, что корни есть. Первый из них (360 градусов) можно отбросить сразу – при таком «раскрое» круглой заготовки объем не максимальный, а минимальный. Второй же «корень» (Root) иллюстрирует принцип: «каков вопрос – таков и ответ». Но если пользователь по-прежнему желает получить аналитический ответ, он должен вернуться к исходной производной и помочь пакету Mathcad решить уравнение, приняв во внимание тот факт, что если один из сомножителей равен нулю, то равно нулю и все произведение. Преобразует же исходное выражение к произведению отдельных сомножителей команда факторизации (Factor), которую мы довольно подробно рассмотрели, анализируя простые числа (рис. 7.11). На рис. 7.31 команда Factor не только нашла произведение, но и упростила выражение для производной, что позволило свести решение к поиску корней квадратного уравнения.

Аналитическая попытка решения задачи о двух ведрах (пункт 2 на рис. 7.31) оборвалась на самом первом шаге – на попытке взятия производной. Но решение у задачи есть, и автор предлагает читателю найти его гибридным методом, комбинируя число, символ и интуицию.

На рис. 7.32. представлено решение задачи о бесконечном числе коробок (см. схему раскроя в пункте 1 на рис. 7.15) с бесконечным числом пропорций выкройки, найденное безо всякого компьютера Б.С. Кушнером из г. Жигулевска Самарской области.

Рис. 7.32. Гибридное решение задачи о коробках

Вторая сторона проблемы повернута, как это ни покажется странным, из области науки в область искусства и даже религии.

Есть люди, способные настроиться на определенный лад, вспоминая любимые стихи, напевая приятную мелодию, мысленно представляя себе живописный пейзаж[58]. А есть счастливчики, расширяющие во время такой душевной медитации список изящного. Они, например, отслеживают про себя побайтный обмен данных на шине компьютера, составляют в голове программу для него или доказывают математическую теорему: Как мысли черные к тебе придут, откупори шампанского бутылку иль пере... реши задачу Коши. Ответ же ищется и численно, и аналитически, и... интуитивно. Присниться может не только таблица химических элементов (и не только Менделееву), но и... неведомое семейство кривых или небывалая структура данных.

По мнению таких «чудаков» (а на них держится настоящая математика), взятие интеграла на ЭВМ равносильно... сочинению стихов на компьютере. И в плане кощунственности самой мысли, и в плане практической, а тем более общеобразовательной (эстетической) пользы. Мы недаром подчеркнули триединство процесса решения задачи. Численные и даже аналитические методы можно отдать на откуп машине. Но интуицию...

[1] Тут правильнее говорить о компьютерной математике аналитических преобразований, но у нас уже прижилась калька с английского термина Symbolic Mathematic ¾ символьная математика.

[2] В пятой версии Mathcad порядок производной не мог быть переменной величиной. В шестом Mathcad’е этот недостаток был исправлен.

[3] Приставка Pro (professional) в названии пакета свидетельствует о том, что в него включены и средства символьной математики.

[4] Это деление не совсем логично: Во-первых, есть еще команды символьных преобразований, требующие указания переменной, к которым они относятся, ¾ преобразование Лапласа, например. Во-вторых, команды Expand (разложить по степеням) и Factor (представить в виде произведения) в их операторных аналогах (см. раздел 7.2) также могут требовать указания переменной, относительно которой данное действие производится.

[5] О том, что проще — x² или x×x, можно еще спорить.

[6] У нас еще говорят «с плавающей десятичной запятой», учитывая тот факт, что на бумаге мы по-прежнему отделяем целую часть от дробной запятой, а не точкой. Из-за этого возможны конфликты при передаче данных из среды Mathcad в среду Excel (см. приложение 9), где нередко при настройке в качестве разделителя в вещественном числе выбирается запятая, а не точка.

[7] Вот полный список таких функций и констант: arcsec, arccsc, arccot, arcsech, arcscsh, arccoth, g, Catalan's constant, Chi(x), Ci(x), csgn(x), dilog(x), Dirac(x), Ei(x), erf(z), FresnelC(x), FresnelS(x), GAMMA(z), hypergeom(n1, n2..., d1, d2..., z), LegendreE(x,k), LegendreEc(k), LegendreEc1(k), LegendreF(x,k), LegendreKc(k), LegendreKc1(k), LegendrePi(x,n,k), LegendrePic(n,k), LegendrePic1(n,k), Psi(n,x), Psi(x), Shi(x), Si(x), signum(x), W(x), W(n,x) и Zeta(s). Если читатель с ними столкнется, работая в среде Mathcad, то ему нужно будет обратиться к help’у.

[8] В шестой и седьмой версиях Mathcad при включении в работу символьного процессора вместо привычного курсора мыши (стрелка) появляется докторская четырехуголка. В четвертой и пятой версиях курсор превращался в кленовый лист: maple по-английски «клен» - фирма Waterloo Maple находится в Канаде.

[9] В сети Internet по адресу ftp.wustl.edu/doc/misc/pi можно найти число π с 1 500 000 знаками.

[10] Напоминаем, что в среде Mathcad 8 Pro недопустимы буквы кириллицы в именах переменных при символьных преобразованиях.

[11] Не к ночи будет упомянут, хотя «крестная мама» диамата — классическая философия Гегеля вдохновила автора на работу над книгой под условным названием «Философия программирования».

[12] В восьмой версии Mathcad невязка уже не показывается, так как от нее мало было толку

[13] Это не команда, а переключатель режимов символьных преобразований.

[14] Ее не любят только две категории людей: ущербные люди, которые никого и ничего любить не могут, и люди, с математикой незнакомые. Но любовь автора к математике, увы, не совсем взаимна. Автор в свое время не получил должного математического образования. Отсюда некоторые, мягко говоря, «нестыковки», которые настоящий математик обязательно увидит в книге. Пример: взятие производной и дифференцирование — это далеко не одно и то же.

[15] ОТЦ — имеются в виду электрические, а не пролетарские цепи. У дисциплины «Основы теории пролетарских цепей» другое название — «Политэкономия капитализма». У нас в МЭИ ОТЦ блестяще читал профессор Карл Круг, о котором рассказывали такую страшилку. Сдает студент экзамен по ОТЦ, а Круг его прерывает и говорит: «Да вы, батенька, не знаете закона Ома. Что у вас по физике?» Круг перелистывал страницы зачетки, видел тройку по физике, зачеркивал ее и говорил обалдевшему студенту: «Сначала выучите и сдайте физику, а уж потом приступайте к моей дисциплине».

[16] Случай, когда без команд символьных преобразований не обойтись, ниже на рис. 7.10.

[17] В настоящее время компьютерными символьными преобразованиями проверяются выкладки великих математиков. Ни одной ошибки не нашли пока только у «короля» математиков — Гаусса (см. раздел 7.3). Компьютерной математикой стоит контролировать свои собственные аналитические выкладки.

[18] Новое — это хорошо забытое старое: см. рис.1.4 в этюде 1.

[19] Константа интегрирования, как мы уже отметили ранее, опускается (полагается равной нулю).

[20] В среде Mathcad PLUS 6.0, который у нас до сих пор очень популярен по двум причинам — наличие русифицированной версии и возможность работы под управлением Windows 3.1 на не очень мощных компьютерах («тройки» и «четверки»), направление символьных преобразований оператором g ® задавалось семью ключевыми словами: (factor, expand, series, simplify, complex, float и assume), которые писались до данного оператора. Это было очень неудобно. Во-первых, в ключевом слове можно было сделать ошибку — написать, например, вместо слова Simplify слово Simplifi. В этой ситуации пакет Mathcad ошибку не фиксирует, но и выражение не упрощает.

[21] Команда Simplify меню Symbolic богаче своего тезки-оператора: командой Simplify можно упростить только часть выражения, отмеченную курсором (см. выше).

[22] Единица не входит в множество «простые числа».

[23] Подпись (электронная или обычная) — это гарантия того, что письмо послано именно тем, чей обратный адрес стоит на конверте. Более того, если нужно будет доказать третьей стороне (судье, например) подлинность сообщения, то это можно сделать так, что ни корреспондент, ни адресат не будут это оспаривать.

[24] Такая идиома встречается во многих книгах. При этом как-то упускается из виду, что через пять-десять лет может быть создан компьютер (транспьютер!), который с данной задачей справится уже за приемлемое время. Для такой работы можно объединить разные компьютеры в сеть. Кроме того, «миллион лет» – это не число, а элемент нечеткого множества «очень долго».

[25] Рекорд (самое большое простое число Мерсенна) на 1 июня 1999 – 2^6772593-1.

[26] Суперкомпьютер, конечно, по меркам 1982 года.

[27] Большая теорема Ферма утверждает, что aⁿ+bⁿ=cⁿ только при n2 (3²+4²=5²).

[28] Это делают, конечно, не в среде Mathcad, а с помощью специальных программ, способных возводить в огромную степень огромные числа. Кстати говоря, функция Ferma с выбранными на рис. 7.11 аргументами работает в среде Mathcad 7, но не работает в среде Mathcad 8. Это к нашему тезису о «капризной бабе» под названием символьная математика.

[29] Мартин Гарднер долгое время редактировал рубрику «Занимательная математика» в этом журнале, материалы которой легли в основу его знаменитых книг.

[30] Числа перемножены не оператором n1×n2=, а командой Вычислить символьной математики.

[31] Название приза зашифровано способом, который использовал еще Юлий Цезарь.

[32] В продаже есть и калькуляторы с символьным процессором (например TI-97).

[33] Если n не указано, то возвращается 20 знаков по умолчанию.

[34] Третье отличие команд символьных преобразований от аналогичных операторов: команда float может вывести до 4000 знаков, оператор — до 250.

[35] В шестой версии Mathcad в ходу был термин «SmartMath» — сообразительная математика.

[36] Символ интеграла — это растянутая буква s, первая в слове summa.

[37] Напоминаем, что в среде Mathcad 8 возможен выбор способа численного интегрирования.

[38] У выражения может быть три режима: а) выражение может быть подсвечено (цвет фона отличается от основного — таким образом можно на данное выражение обратить внимание пользователя); б) выражение может быть выключено из расчетов (стать простым комментарием) и в) выражение может быть оптимизировано.

[39] В шестой версии Mathcad командой на локальную оптимизацию служило ключевое слово optimize, поставленное перед выражением. Ключевое слово literally отменяло оптимизацию следующего за ним выражения при включенном режиме глобальной оптимизации. В среде Mathcad 8 также можно включить режим оптимизации всех выражений, а затем через флажок Enable Optimization отключить оптимизацию у некоторых формул.

[40] Намек на то, что самые лучшие математики — это советские евреи.

[41] Становится меньше не только математиков, готовящихся к занятиям, но и просто хороших математиков. Печальная шутка: «Что такое американский университет? Это место, где бывший советский (вспомним красную шестиугольную звездочку на рис. 7.14) на ломаном английском преподает математику китайцам».

[42] Есть горе от ума, а есть горе от компьютеров и, вообще, от горе всяческих плодов цивилизации.

[43] Пример спортивного тренажера казался автору вполне удачным до тех пор, пока он не узнал, что современные тренажеры (тот же Ketler, мелькающий в рекламе по TV) на самом деле оборудованы силовыми приводами, помогающими человеку или тормозящими рычаги в нужный момент. Этим настоящие тренажеры отличаются от простого троса, перекинутого через блок, с грузом на конце.

[44] Этот документ работает в среде Mathcad 7 и не работает в среде Mathcad 8. Ошибки программирования исправлены по принципу «Есть оператор — есть проблема, нет оператора — нет проблемы».

[45] Разработка фирмы Waterloo Maple, Inc., 450 Phillip Street, Waterloo, ON, Canada, N2L 5J2, тел.: 519-747-23, факс: 519-747-5284, http://www.maplesoft.com. Символ V в названии пакета – это латинская буква V (Victory – победа). Далее в тексте мы ее будем опускать – в новейшей версии этого пакета она также опущена – Maple 6. В конце приложения 1 указано, что в Mathcad встроен MKM (MathSoft Kernel Maple), разработанный фирмой Waterloo Maple, Inc.

[46] С другой стороны, «настоящие» научные дисциплины не боятся прилагательного «занимательный»: занимательная математика, занимательная физика и т.д. Но! «Занимательный научный коммунизм» — как вам это понравится?.. Ладно, не будем пинать издыхающего льва — «Занимательная астрология».

[47] Развитие пакета Mathcad для компьютеров Apple Macintosh остановилось на пятой версии, а для DOS — на версии 2.51.

[48] Это был своеобразный протест против господства числа в Computer Science.

[49] Автор давным-давно написал статью о принципах расцвечивания программ и послал ее в журнал «Микропроцессорные средства и системы» (в то время единственный, где публиковались статьи по персональным компьютерам). Статья попала на рецензию… к дальтонику.

[50] Этот принцип применительно к работе на компьютере можно переиначить так: не спеши изучать языки программирования — очень вероятно, что этого не понадобится: программные среды Mathcad и Maple позволяют решать довольно сложные задачи без традиционного кодирования алгоритмов.

[51] В среде языка BASIC ключевое слово print можно заменить знаком вопроса, а в среде Maple совсем опустить — сравните рис. 7.21 и 7.22.

[52] Еще раз напомним, что вычислительная математика Mathcad допускает буквы кириллицы в именах переменных и функций. В символьной математике и Mathcad и Maple этого делать нельзя. Поэтому на рис. 7.24 мы работаем не с переменной Пр, а с переменной Pr.

[53] Приводим цены во французских франках (5 франков » 1 доллар США) из рекламы, помещенной в журнале La Recherche (№ 10’96): Maple V Release 4 — 6450 (3490 — для учебных заведений), Mathcad 6.0 PLUS — 3490, Mathcad 6.0 — 1490. Но самый дорогой математический пакет — это, конечно, Mathematica 3.0 — 8950 (6965). В Москве у фирмы SoftLine (тел. 232-00-23) учебные заведения могут купить Maple за 600 долл., а Mathcad (русскую версию) — за 420 долл. — см. рекламу в конце книги.

[54] Многие молодые читатели их не застали, поэтому автор излагает здесь азы кибернетики.

[55] Главная причина смерти АВМ в том, что на цифровой машине можно смоделировать аналоговую, а на аналоговой цифровую — нет.

[56] Или гибридностью, если вспомнить название раздела книги.

[57] Это возможно только в седьмой версии Mathcad. В более ранних версиях команды символьных преобразований из меню Symbolic с вложенными пользовательскими функциями не работали.

[58] Умный человек никогда не будет скучать с самим собой.