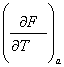63. Рівняння Ван-дер-Вальса. Їзотерми Ван-дер-Вальса. Взаємні
перетворення пари та рідини.
65. Внутрішня енергія газу Ван – дер – Ваальса.
68. Рідини, дифузія, в’язкість.
71.Кривизна
поверхні і додатковий тиск . Формула Лапласа . Капілярні явища
72.Капілярно-гравітаційні хвилі. (Доведення)
73.Кристалічний та аморфний стан речовини.
74. Просторові кристалічні гратки. Сингонії. Гратки Браве.
75. Атомні площини. Індекси Міллера.
76 . Поверхнева енергія і зовнішня форма кристала . Закон
Кюрі та Вульфа .
77. Класифікація кристалів за типами зв’язку в кристалічній
гратці.
80. Квантова теорія теплоємності твердих тіл Планка-Енштейна.
81. Квантова теорія теплоємності твердих тіл Дебая-Борна .
Температура Дебая.
83. Кипіння та конденсація на ядрах.. Камера Вільсона,
бульбашкова камера.
84. Фазові переходи II роду. Співвідношення Ернста
85. Рідкі розчини. Закон Генрі. Закон Рауля. Наслідки
з них.
58. Теорема Нернста. Формулювання третього начала термодинаміки. Наслідки із третього начала термодинаміки.
Теорема Нернста:
При
прямуванні температури до абсолютного нуля, зміна ентропії прямує до деякої
кінцевої межі, яка не залежить від значень параметрів, що визначають рівноважний
стан системи.
![]()
![]() - Формулювання Планка.
- Формулювання Планка.
Дов. S=k*ln(G) – термодинамічна ймовірність (кількість мікростанів, через які можна
представити даний мікростан)
(ɦw/2 – енергія нульових коливань, якою нехтують.)
Т = 0, k->G=1-> lnG =0 -> S=0.
Формулювання 1:
Абсолютний нуль недосяжний, адже тоді можна було б
створити машину ККД
якої рівна 100%.
,
Т2 = 0
-> ![]() = 1 -> неможливо за ІІ началом
термодинаміки
= 1 -> неможливо за ІІ началом
термодинаміки
Формулювання 2 :Неможливо створити вічний двигун
ІІІ роду.
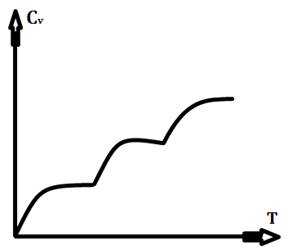 Наслідки
3 начала термодинаміки:
Наслідки
3 начала термодинаміки:
1). При
наближенні температури до 0(К), будь-яка теплоємність прямує до 0.
V = const
бQ
= CvdT
dS = бQ / T = CvdT
/ T;
S – S0 =
![]()
S = S0 + ![]() =
= ![]()
![]() S =
S = ![]()
Cv = V
= ![]() V =
V = 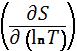 V Т ->
0, lnT -> -∞, Cv ->0.
V Т ->
0, lnT -> -∞, Cv ->0.
Cp = Cv + R – для ідеальних газів
2). При наближенні температури до
абсолютного нуля, ізотерма співпадає з адіабатою:
PV = const, ![]() ,
,
γ = (Cp / Cv) -> 1.
59.Метод термодинамічних потенціалів. Внутрішня енергія як термодинамічний потенціал. Співвідношення Максвела.
Метод термодинамічних потенціалів допомагає перетворювати вирази, в які входять основні термодинамічні величини, такі як кількість теплоти, ентропію, внутрішню енергію через величини, які можна поміряти – температуру, тиск та об’єм.
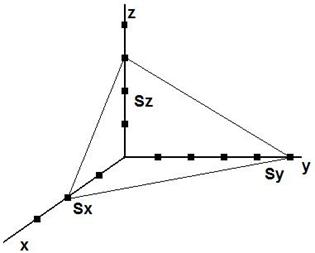
Якщо розглядати внутрішню енергію U Розглядати як потенціальну енергію, виражену через незалежні змінні S i V, то можна вважати вн. енергію термодинамічним потенціалом.
Тоді для U=U(S, V) отримуємо співвідношення
Максвела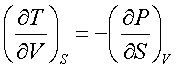
60.Метод термодинамічних потенціалів. Вільна енергія як термодинамічний потенціал. Співвідношення Максвела і рівняння Гіббса-Гельмгольца.
Метод термодинамічних потенціалів допомагає перетворювати вирази, в які входять основні термодинамічні величини, такі як кількість теплоти, ентропію, внутрішню енергію через величини, які можна поміряти – температуру, тиск та об’єм.
Якщо розглядати вільну енергію F як величину, виражену через незалежні змінні V i T, то можна вважати вільну енергію термодинамічним потенціалом.
Тоді для F=F(V, T) отримуємо
співвідношення Максвела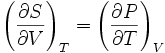 .
.
За рівнянням Гіббса-Гельмгольца вільна енергія визначається так:
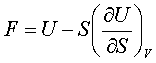 .
.
61.Метод термодинамічних потенціалів. Ентальпія як термодинамічний потенціал. Співвідношення Максвела і рівняння Гіббса-Гельмгольца.
Метод термодинамічних потенціалів допомагає перетворювати вирази, в які входять основні термодинамічні величини, такі як кількість теплоти, ентропію, внутрішню енергію через величини, які можна поміряти – температуру, тиск та об’єм.
Якщо розглядати ентальпію I як величину, виражену через незалежні змінні S i P, то можна вважати вільну енергію термодинамічним потенціалом.
Тоді для U=U(S, P) отримуємо співвідношення
Максвела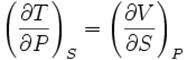
За рівнянням Гіббса-Гельмгольца ентальпія
визначається так: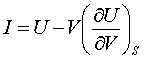 .
.
62. Метод термодинамічних потенціалів. Термодинамічний потенціал Гібса. Співвідношення Максвелла і рівняння Гібса-Гельмгольца.
Якщо
процес квазістатичний, то ![]() . Для такого процесу рівняння першого начала
термодинаміки
. Для такого процесу рівняння першого начала
термодинаміки ![]()
Можна
представити у вигляді ![]()
Якщо
ввести ентальпію ![]() , то можна виключити
, то можна виключити ![]() та отримати
та отримати ![]()
В термодинаміку було введено дві важливі функції: вільна енергія F, введена Гельмгольцем, і термодинамічний потенціал G , введений Гібсом. Ці функції виражаються співвідношенням
F=U-TS (1), G=F+PV=U-TS+PV .(2)
Їх диференціали ![]() При ізотермічному процесі dT=0, а тому dF = - PdV = -
δA. Звідси A=F1-F2 .Отже,
вільна енергія є функцією стану системи, втрати якої в квазистатичномуу процесі
дають роботу, зроблену системою. Термодинамічний потенціал Гібса слід розглядати як функцію від T i P: G=G(T,P) (3). Такого роду
співвідношення називається канонічним
рівнянням стану речовини. Канонічне
рівняння стану, містить повний обсяг
інформації про термічні та калоричні властивості речовини.
При ізотермічному процесі dT=0, а тому dF = - PdV = -
δA. Звідси A=F1-F2 .Отже,
вільна енергія є функцією стану системи, втрати якої в квазистатичномуу процесі
дають роботу, зроблену системою. Термодинамічний потенціал Гібса слід розглядати як функцію від T i P: G=G(T,P) (3). Такого роду
співвідношення називається канонічним
рівнянням стану речовини. Канонічне
рівняння стану, містить повний обсяг
інформації про термічні та калоричні властивості речовини.
![]() (4) З цього рівняння
(4) З цього рівняння![]() З означення функції
F i G слідує U=F+TS, I=G+TS. Підставив вираз ентропії
З означення функції
F i G слідує U=F+TS, I=G+TS. Підставив вираз ентропії ![]() . Це рівняння називається рівнянням Гібса-Гельмгольца.
Далі вторинним диференціюванням із співвідношення (4) знаходимо
. Це рівняння називається рівнянням Гібса-Гельмгольца.
Далі вторинним диференціюванням із співвідношення (4) знаходимо ![]() Це
співвідношення називається співвідношенням Максвелла. Воно використовується для
виводу різних співвідношень між величинами, що характеризують термодинамічно
рівноважні стани системи. Такий метод
називається методом термолинамічних потенціалів.
Це
співвідношення називається співвідношенням Максвелла. Воно використовується для
виводу різних співвідношень між величинами, що характеризують термодинамічно
рівноважні стани системи. Такий метод
називається методом термолинамічних потенціалів.
63. Рівняння Ван-дер-Вальса. Їзотерми Ван-дер-Вальса. Взаємні перетворення пари та рідини.
 Рівняння
Рівняння 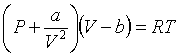 називається
рівнянням стану реального газу, або рівнянням Ван-дер-Ваальса. Поправки a і b
називаються сталими Ван-дер-Ваальса і залежать від природи газу. Це рівняння
описує стан одного моля реального газу. Якщо розглядати довільну кількість газу
масою
називається
рівнянням стану реального газу, або рівнянням Ван-дер-Ваальса. Поправки a і b
називаються сталими Ван-дер-Ваальса і залежать від природи газу. Це рівняння
описує стан одного моля реального газу. Якщо розглядати довільну кількість газу
масою ![]() , то рівняння можна переписати так:
, то рівняння можна переписати так: ![]() . Доданок в перших дужках враховує взаємодію молекул
газу, а в других – розміри молекул.
Порівнюючи рівняння Ван-дер-Ваальса з рівнянням стану ідеального газу (
. Доданок в перших дужках враховує взаємодію молекул
газу, а в других – розміри молекул.
Порівнюючи рівняння Ван-дер-Ваальса з рівнянням стану ідеального газу (![]() ), приходимо до висновку, що ізотерми реального газу
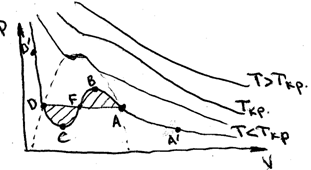
відрізняються від ізотерм ідеального. Типові ізотерми Ван-дер-Ваальса наведено
на рис. Кожному значенню тиску відповідає одне або три значення об‘єму (в
ідеальному газі тільки одне). Оскільки рівняння Ван-дер-Ваальса
для реального газу є многочленом 3 степення відносно V, то для різних P при
T=const буде 1 або 3 різні значення V. Експериментальні ізотерми T>Tкр
збігаються з теор. А при T<Tкр є деякі відмінності. На CB тиск (P) росте із
ростом об’єму (V)
), приходимо до висновку, що ізотерми реального газу
відрізняються від ізотерм ідеального. Типові ізотерми Ван-дер-Ваальса наведено
на рис. Кожному значенню тиску відповідає одне або три значення об‘єму (в
ідеальному газі тільки одне). Оскільки рівняння Ван-дер-Ваальса
для реального газу є многочленом 3 степення відносно V, то для різних P при
T=const буде 1 або 3 різні значення V. Експериментальні ізотерми T>Tкр
збігаються з теор. А при T<Tкр є деякі відмінності. На CB тиск (P) росте із
ростом об’єму (V) ![]() Ясно, що ні в одній точці система не може бути в
рівновазі. Тому CB існує не стійко. В областях D’DC і BAA’
Ясно, що ні в одній точці система не може бути в
рівновазі. Тому CB існує не стійко. В областях D’DC і BAA’ ![]() . Тому ці стани стійкі. Отже, цікаво, як може система
перейти з однієї області в іншу через нестійку область. Експеримент показав,що
на цьому етапі ізотерма в натурі горизонтальна DA. Перейдемо з D в A оборотньо
двома шляхами – DFA і DCFBA.
. Тому ці стани стійкі. Отже, цікаво, як може система
перейти з однієї області в іншу через нестійку область. Експеримент показав,що
на цьому етапі ізотерма в натурі горизонтальна DA. Перейдемо з D в A оборотньо
двома шляхами – DFA і DCFBA.
Тоді:
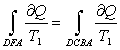 , оск. T1=const ,
, оск. T1=const , ![]() Отже DFA повинна
бути так розміщена, щоб
Отже DFA повинна
бути так розміщена, щоб ![]() а отже
відповідні площі під кривими DFA і DCBA повинні бути однакові. Ясно, що A’A і DD’ – газоподібний та рідкий стани. На
AB і CD відповідно – переохолоджена пара та перегріта рідина. Ці стани
метастабільні, тобто нестійкі. Переохолоджена пара – це стан речовини коли по
параметрам має бути рідина але є газ (має властивості газу – заповнює весь
об’єм і т.д. ), а перегріта рідина відповідно – коли по параметрам має бути газ
а є рідина (по властивостям).
а отже
відповідні площі під кривими DFA і DCBA повинні бути однакові. Ясно, що A’A і DD’ – газоподібний та рідкий стани. На
AB і CD відповідно – переохолоджена пара та перегріта рідина. Ці стани
метастабільні, тобто нестійкі. Переохолоджена пара – це стан речовини коли по
параметрам має бути рідина але є газ (має властивості газу – заповнює весь
об’єм і т.д. ), а перегріта рідина відповідно – коли по параметрам має бути газ
а є рідина (по властивостям).
64.Критичний стан. Критичні параметри. Методи визначення критичних параметрів. Зведене рівняння Ван-дер-Вальса.
При певних параметрах T,P існує тільки одне
рішення рівняння Ван-дер-Ваальса. Така ізотерма наз. критичною, при цьому зникає різниця між газом і рідиною і цей стан
речовини наз. критичним станом. Оцінити
критичні параметри можна на підставі
рівняння В-дер-В. Перепишемо його так:![]() , У критичній точці
, У критичній точці 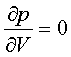 ,
,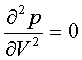 знайдемо це:
знайдемо це: 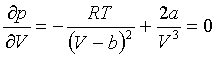 ,
, 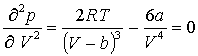 , З цих двох рівнянь знаходимо
критичні параметри:
, З цих двох рівнянь знаходимо
критичні параметри: ![]() ,
, 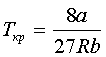 ,
, 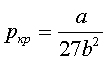 . Щоб знайти сталі a, b для різних газів на
експерименті фіксуються критичні параметри газів, бо теоретично отримати
значення цих сталих з рівняння В-дер-В неможливо. Щоб перевірити правильність
рівняння В-дер-В знайдемо величину
. Щоб знайти сталі a, b для різних газів на
експерименті фіксуються критичні параметри газів, бо теоретично отримати
значення цих сталих з рівняння В-дер-В неможливо. Щоб перевірити правильність
рівняння В-дер-В знайдемо величину 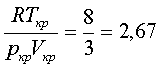 . Експеримент дає такі значення: водень – 3,28; кисень
– 3,42. Це розходження свідчить про те, що рівняння В-дер-В, яке виведено з
припущення, що молекули – це тверді кулі, є неточним.
. Експеримент дає такі значення: водень – 3,28; кисень
– 3,42. Це розходження свідчить про те, що рівняння В-дер-В, яке виведено з
припущення, що молекули – це тверді кулі, є неточним.
Зведене
рівняння. Треба отримати рівняння стану незалежно від
природи газу, тобто універсальне. Будь-які гази з однаковим(відповідним)
відношенням 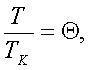
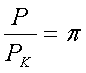 ,
, 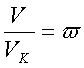 будуть описуватися ідентичними рівняннями. Параметри
будуть описуватися ідентичними рівняннями. Параметри ![]() називають зведеними.
називають зведеними.![]() ,
, 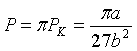 ,
, ![]()
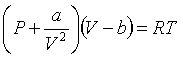
![]()
![]()
У даному рівнянні немає констант для окремих газів. Воно називається зведеним рівнянням стану. З нього випливає, що якщо гази мають два однакові зведені параметри з трьох, то й третій параметр для них однаковий. Цей закон називається законом відповідних станів.
65. Внутрішня енергія газу Ван – дер – Ваальса.
Ця енергія складається із внутрішньої енергії,
які складають газ, і кінетичної енергії руху ценру мас молекул (СvT), і із потенціальної
енергіївзаємного притягування молекул , яка має відємне значення. Потенціальна
енергія протягування рівна роботі , яку необхідно затратити проти сил
протягування для того, щоб розвести молекули на нескінчену відстань одної від
одної, коли взаємодію між ними можна вважати відсутню, а потенціальну енергію
взаємодії – рівну нулю. Тиск за рахунок притягання між молекуламив рівняні
Ван-дер-Ваальса рівне а/V2, і
звідси потенціальна енергія:
Еп = ![]()
Внутрішня енергія газу Ван-дер Ваальса :
dU = CVdT +
[T(dp/dT)v-p]dV
Із рівнянь Ван-дер-Ваальса:
p = RT/(V-b) – a/V2
T(dp/dT)v =
RT/(V - b) = p + a/V2
dU = Cv dT +
(a*dV)/V2
Вважаючи що U=0 при Т=0 і
V=∞, отримаємо:
U = CVT-a/V,
де СV не залежить від Т.
66. Ефект Джоуля-Томсона.
(62.
Ефект Джоуля-Томпсона для газу Ван-дер-Ваальса. Температура інверсії. Пояснення
єфекту; 63. Досліди Гей-Люссака, Джоуля і Томпсона по визначенню залежностей
внутрішньої енергії газу від об”єму. Використання методу циклів для вирішення
цієї задачі)
Еф.Д-Т полягає в зміні температури реального
газу при його адіабатному дроселюванні (повільному протіканні газу крізь
перешкоду, напр.. пористий корок) - розширенні без виконання роботи. При такому
розширенні енергія газу залишається незмінною, а відбувається взаємний перехід
між кінетичною і потенціальною її складовими. Якщо перед розширенням у газі
переважало притягання молекул (потенціальна енергія при цьому була від‘ємною),
то при значних розширеннях вона зростатиме за рахунок кінетичної енергії
молекул і газ охолоджуватиметься (додатний еф.Д-Т). Якщо ж перед розширенням
домінувало відштовхування молекул (потенціальна енергія додатна), то при
розширенні вона зменшиться , а кінетична збільшиться і газ нагріється
(від‘ємний еф.Д-Т). Той самий газ, залежно від тиску і температури, може
виявити як додатний, так і від‘ємний еф.Д-Т. Той стан газу, при якому його
розширення не веде до зміни температури (еф.Д-Т відсутній) наз. точкою
інверсії, а температура, за якої Еф.Д-Т був відкритий у 1853 р. ,
застосовується при зрідженні газів. Щоб при черговому розширенні газ
охолоджувався, його треба охолодити нижче від точки інверсії.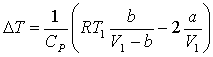 , де
, де ![]() - температура охолодження газу,
- температура охолодження газу, ![]() -початкова температура,
-початкова температура, ![]() - об‘єм газу до розширення,
- об‘єм газу до розширення, ![]() - сталі в рівнянні
Ван-дер-Ваальса. При інверсії
- сталі в рівнянні
Ван-дер-Ваальса. При інверсії ![]() , отже температура інверсії
знаходиться з рівняння:
, отже температура інверсії
знаходиться з рівняння: ![]()
Пояснення ефекту Д-Т: Для реального газу
внутрішня енергія складається з кінетичної енергії молекул і потенціальної
енергії їхньої взаємодії між собою. Потенціальна енергія знаходиться з рівняння
Ван-дер-Ваальса 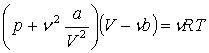 наступним чином:
наступним чином: 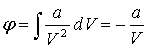 , отже для внутрішньої енергії
реального разу
, отже для внутрішньої енергії
реального разу ![]() . відсутнє еф.Д-Т наз.
температурою інверсії.Суть досліду полягає в тому, що збільшення кінетичної
енергії молекул (отже і температури) відбувається за рахунок зміни
потенціальної енергії взаємодії молекул. Внутрішня енергія газу залишається
незмінною, а енергія перерозподіляється між першим і другим доданками. Ідея
досліду: у добре ізольовану трубку поміщали пробку з вати. З одного боку від
цієї пробки був газ під тиском
. відсутнє еф.Д-Т наз.
температурою інверсії.Суть досліду полягає в тому, що збільшення кінетичної
енергії молекул (отже і температури) відбувається за рахунок зміни
потенціальної енергії взаємодії молекул. Внутрішня енергія газу залишається
незмінною, а енергія перерозподіляється між першим і другим доданками. Ідея
досліду: у добре ізольовану трубку поміщали пробку з вати. З одного боку від
цієї пробки був газ під тиском ![]() , а з другого під тиском
, а з другого під тиском ![]() . Внаслідок різниці тисків газ
протискувався через корок, розширюючись адіабатно. З обох боків пробки
вимірювали температуру. Для більшості газів температура при цьому
збільшувалась. “Протискування” газу через пробку вимагає витрат роботи
. Внаслідок різниці тисків газ
протискувався через корок, розширюючись адіабатно. З обох боків пробки
вимірювали температуру. Для більшості газів температура при цьому
збільшувалась. “Протискування” газу через пробку вимагає витрат роботи ![]() . Пізніше під час розширення газ
сам виконує роботу
. Пізніше під час розширення газ
сам виконує роботу ![]() , причому
, причому ![]() . В лівій частині рівняння газ можна вважати
реальним, в правій частині – можна газ прийняти за ідеальний (спрощення). Для
реального газу (ліва частина) матиме:
. В лівій частині рівняння газ можна вважати
реальним, в правій частині – можна газ прийняти за ідеальний (спрощення). Для
реального газу (ліва частина) матиме:![]() , а
, а ![]() .
.
Прирівнюючи ці величини дістанемо рівняння з
якого можна знайти![]()
![]()
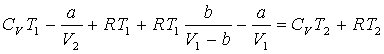
67.Зрідження газів і методи одержання низьких температур(Джоуля-Томпсона, адіабатного розширення, адіабатного розмагнічення). Машини Клода і Лінде.
В техніці для зрідження газів використовуються такі основні методи: 1)випаровування рідини(так працюють домашні холодильники), метод заснований на ефекті пониження тем-ри при випаровуванні; 2)Адіабатичне розмагнічення - деякі речовини (парамагнетики) мають здатність зберігати свій магнітний момент. При намагнічуванні у таких речовин потенційна енергія взаємодії зменшується. Охолодимо деякий намагнічений парамагнетик і адіабатично розмагнітимо його. При повільному розмагнічуванні ентропія системи незмінна(процес оборотний), з іншого боку внаслідок зростання ентропії, пов’язаної з розмагніченням спадає ентропія теплового руху (іде ще більше охолодження).
3)використання ефекту Джоуля-Томпсона- ідея методу полягає в тому, що газ пропускають через деяку пористу перегородку (дроселювання), підтримуючи сталу різницю тисків. Ефект має місце лише для реальних газів. При цьому в залежності від початкової тем-ри (тем-ри інверсії) газ може як нагріватися так і охолоджуватися. 4)адіабатне розширення газу з виконанням зовнішньої роботи-ідея цього методу слідує з рівняння адіабати. Метод адіабатного розширення є більш ефективним, оскільки він придатний і для реальних газів. Це пояснюється тим, що у випадку ідеальних газів робота виконується за рахунок внутрішньої енергії, а вона є монотонно зростаючою функцією самої лише тем-ри. Якщо енергії для виконання роботи не вистачає, роботу можна виконувати над тілом (наприклад розширяти поршень мотором), охолодження все одно відбуватиметься.
Машина Клода - використовує адіабатичне розширення і є більш ефективною
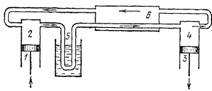 Поршнем 1 газ подають в установку, перетікаючи з циліндра 2 по трубкам
5, газ охолоджується за допомогою води (або іншого холодильника), і потрапляє в
теплообмінник, де він охолоджується завдяки теплообміну з більш холодним газом.
Потім газ потрапляє в детандер 4, де зазнає адіабатичного розширення і ще більш
охолоджується. Далі газ потрапляє до поршня 2 через теплообмінник 6 і цикл
повторюється, поки не настане зрідження.
Поршнем 1 газ подають в установку, перетікаючи з циліндра 2 по трубкам
5, газ охолоджується за допомогою води (або іншого холодильника), і потрапляє в
теплообмінник, де він охолоджується завдяки теплообміну з більш холодним газом.
Потім газ потрапляє в детандер 4, де зазнає адіабатичного розширення і ще більш
охолоджується. Далі газ потрапляє до поршня 2 через теплообмінник 6 і цикл
повторюється, поки не настане зрідження.
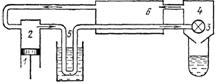 Машина Лінде - повністю аналогічна машині Клода, але замість
детандера в ній стоїть вентиль, завдяки
чому відбувається дроселювання.
Машина Лінде - повністю аналогічна машині Клода, але замість
детандера в ній стоїть вентиль, завдяки
чому відбувається дроселювання.
68. Рідини, дифузія, в’язкість.
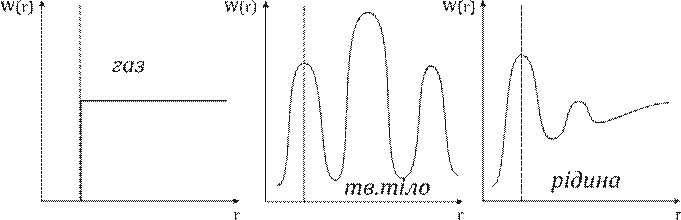 Особливості рідкого стану, модель рідини.
Особливості рідкого стану, модель рідини.
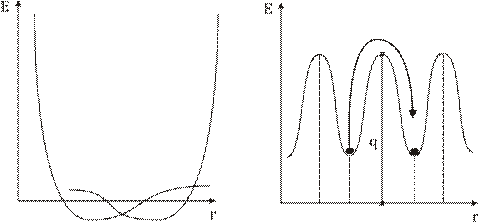
q – висота потенціального бар’єру
Тепловий рух у рідинах.
τ – час осідлого життя молекул, час знаходження мол. в потенціальній ямі.
![]()
![]()
j – кількість стрибків; а– const; ν – частота коливань молекул в ямі
 1 еВ = 1,6 * 10-19
Дж
1 еВ = 1,6 * 10-19
Дж
![]()
![]()
![]()
![]()
![]()
![]()
Явища переносу у рідинах
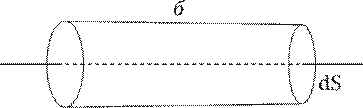 dN – кількість молекул, що
проходить за одиницю часу через площадку dS
dN – кількість молекул, що
проходить за одиницю часу через площадку dS
![]()
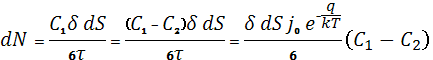
…(далі зі шпор…)
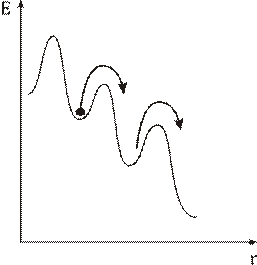
В розташуванні частинок рідини спостерігається ближній порядок. Тобто, по відношенню до будь-якої частинки розташування найближчих до неї сусідів є впорядкованим. Через це структуру рідин називають квазікристалічною. Теорія рідин менш розвинута ніж теорія будови газу чи кристалу через проміжний? стан рідин. Найбільший вклад в розбудову теорії рідин зробив Френкель. Згідно з Френкелем, тепловий рух в рідинах має наступний характер. Кожна молекула на протязі деякого часу коливається коло визначеного положення рівноваги. Час від часу молекула змінює місце рівноваги, стрибком переміщуючись в нове положення, що знаходиться на відстані порядку розмірів молекули від попереднього. Таким чином, молекули лише повільно переміщуються всередині рідини, перебуваючи частину часу біля визначених місць. Довжина часу стоянки молекули є досить різними і хаотично чергуються, але середня величина коливань навколо одного й того самого положення рівноваги є у кожної рідини певної величини, що різко зменшується з підвищенням температури. В зв’язку з цим при підвищенні температури сильно збільшується рухомість молекул, що в свою чергу призводить до зменшення в’язкості рідин.
В’язкість рідин виникає при русі рідини через
перенос імпульсу в напрямі, перпендикулярному до напряму руху. Перенос імпульсу
здійснюється при стрибках молекул, про які вже говорилось вище. Загальний закон
внутрішнього тертя: ![]() . Рідина буде тим більш текучою (з меншою в’язкістю),
чим менший час t стоянки молекул і Þ чим частіше відбуваються стрибки. Ці міркування призводять до рівняння
Френзеля-Андраде для коефіцієнту в’язкості:
. Рідина буде тим більш текучою (з меншою в’язкістю),
чим менший час t стоянки молекул і Þ чим частіше відбуваються стрибки. Ці міркування призводять до рівняння
Френзеля-Андраде для коефіцієнту в’язкості: ![]() . Множник С, що входить у
це рівняння, залежить від відстані стрибка d, частоти коливань v і
температури. Однако, температурний хід в’язкості визначається множником
. Множник С, що входить у
це рівняння, залежить від відстані стрибка d, частоти коливань v і
температури. Однако, температурний хід в’язкості визначається множником ![]() . Þ з температури в’язкість швидко ¯. Так, в’язкість води при зміні
температури від 0°С до 100°С зменшується від 1,8х10-3 до 2,8х10-4 кг/м×с. Вимірюється цей коефіцієнт за
допомогою віскозіметра.
. Þ з температури в’язкість швидко ¯. Так, в’язкість води при зміні
температури від 0°С до 100°С зменшується від 1,8х10-3 до 2,8х10-4 кг/м×с. Вимірюється цей коефіцієнт за
допомогою віскозіметра.
Частіше вони побудовані на принципі
спостереження стоку рідини через капіляри, швидкість якого залежить від
в’язкості по закону Пуазейля: 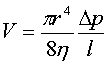 . Тут: V – об’єм
рідини, що протікає в одиницю часу через капіляр радіусом r під дією
різниці тисків Dр при довжині капіляру l.
. Тут: V – об’єм
рідини, що протікає в одиницю часу через капіляр радіусом r під дією
різниці тисків Dр при довжині капіляру l.
В
рідині є істинним закон Фіка (загальне рівняння явищ переносу): ![]() . Коеф. дифузії можна отримати з наступних міркувань:
якщо час між стрибками молекул позначити через t, то величина d/t є швидкість молекули. Це дозволяє порівняти
. Коеф. дифузії можна отримати з наступних міркувань:
якщо час між стрибками молекул позначити через t, то величина d/t є швидкість молекули. Це дозволяє порівняти ![]() з середньою довжиною вільного пробігу, а
з середньою довжиною вільного пробігу, а ![]() - з середньою швидкістю молекул. Þ Коеф. самодифузії рідини:
- з середньою швидкістю молекул. Þ Коеф. самодифузії рідини: ![]() . Множник 1/6 є тому, що рух носить хаотичний характер,
тому можливі 6 напрямів руху молекули. Кількість молекул в одному напрямі є
(1/6)n0. В формулу входить середнє значення
квадрату, а не квадрат середнього значення (див. початок 2-го семестру з
фізики). Коеф. D залежить від Т тому, що з Т - ¯ час “спокійного” життя молекули, що
призводить до D. Час перебування молекули в даному місці рідини визначається
ймовірністю для молекули отр. енергію w, необхідну для стрибка. Ця ймовірність визн. законом Больцмана:
. Множник 1/6 є тому, що рух носить хаотичний характер,
тому можливі 6 напрямів руху молекули. Кількість молекул в одному напрямі є
(1/6)n0. В формулу входить середнє значення
квадрату, а не квадрат середнього значення (див. початок 2-го семестру з
фізики). Коеф. D залежить від Т тому, що з Т - ¯ час “спокійного” життя молекули, що
призводить до D. Час перебування молекули в даному місці рідини визначається
ймовірністю для молекули отр. енергію w, необхідну для стрибка. Ця ймовірність визн. законом Больцмана: 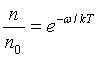 . Тут п –
число молекул в об’ємі, енергія яких w, а п0 – число молекул, що мають середню теплову
енергію, або kT. Þ
. Тут п –
число молекул в об’ємі, енергія яких w, а п0 – число молекул, що мають середню теплову
енергію, або kT. Þ ![]() . Множник А має сенс періода коливань молекули
(А=1/v). Підставивши в формулу для коеф. дифузії, отр.:
. Множник А має сенс періода коливань молекули
(А=1/v). Підставивши в формулу для коеф. дифузії, отр.: ![]() . Тут
. Тут ![]() , а w - енергія, що необхідна для стрибка молекули, що наз. енергією
активації молекули. Числове значення коеф. дифузії у рідин << ніж у
газів.
, а w - енергія, що необхідна для стрибка молекули, що наз. енергією
активації молекули. Числове значення коеф. дифузії у рідин << ніж у
газів.
69.Явище поверхневого натягу
Рідкий стан утворюється тоді, коли потенціальна енергія притяжіння молекул переважає над їх потенціальною енергією. Таким чином у рідин утворюється поверхність, котра обмежує її об`єм. На частини, котрі знаходяться поблизу поверхні, діють зі сторони інших молекул рідини сили, рівнодійна яких, направлена в середину рідини нормально до поверхні. Для збільшення поверхні рідини потрібно виконати роботу. При Т=const роль потенціальної енергії грає вільна енергія Е, для якої правдиве відношення dE=-dA? Де dA – робота, пов’язана з виникненням вільної енергії. В результаті однорідності поверхні вільна енергія ~ S(площі). Тому E=ss , де s -питома густина вільної енергії поверхні. Так як і в механіці, система прямує до мінімальної потенціальної енергії. В термодинаміці система прямує до мінімуму вільної енергії. Тому поверхня рідини намагається скоротитись. Завдяки цьому вздовж поверхні рідини діють сили , котрі називаються силами поверхневого натягу.
Робота, яку треба виконати щоб ізотермічно, квазістатично збільшити поверхню рідини на одиницю, при незмінному об`ємі, називається коефіцієнтом поверхневого натягу, або поверхневим натягом.
dF=-SdT – pdV (SdT=0)
dF=-pdV=-δA
F=Fоб+ Fпов
f1=f(V) f1-обємна густина
вільної енергії
Fпов=(f2)a
f2=s s - коефіцієнт
поверхневого натягу
|
δQ=dU+δA dA
TdS=dU- sda sda F=U-TS -sda dF=dU-TdS-SdT
dU-TdS=sda
dF=sda-SdT
S= U=F-T U=F-T F=s a |
U=s a-T ∆Q=∆U-s∆ a ∆Q=s∆ a-T q= |
70. Крайові кути.Змочування.Умови рівноваги на межі трьох рідин та на межі рідини з іншим середовищем.
Припустимо три
рідких середовища(1,2,3)попарно межують для рівноваги потрібно,щоб всі
сили,які діють на рідину всередині циліндра S,урівноважувались.Ці сили
складаються з сил поверхневого натягу![]() ,сил гідростатичного тискуна поверхність S та сили тяжіння
рідини,замкненої всередині об’єму, обмеженого даною поверхнею.Силою тяжіння і
гідростатичним тиском можна знехтувати і записати відповідне рівняння:
,сил гідростатичного тискуна поверхність S та сили тяжіння
рідини,замкненої всередині об’єму, обмеженого даною поверхнею.Силою тяжіння і
гідростатичним тиском можна знехтувати і записати відповідне рівняння:![]() (2)з собою вздовж трьох поверхонь,які перетинаються вздовж деякої лінії
О.Приклад:крапля на поверхні іншої рідини.(мал)При цьому векторна умова рівноваги
(2) розпадається на два скалярних рівняння:
(2)з собою вздовж трьох поверхонь,які перетинаються вздовж деякої лінії
О.Приклад:крапля на поверхні іншої рідини.(мал)При цьому векторна умова рівноваги
(2) розпадається на два скалярних рівняння:![]()
![]()
![]() ;
;
З них отримуємо:![]() ;
;![]()
Цими формулами визнач. кути ![]() . Рівновага можлива ,коли
. Рівновага можлива ,коли <
<![]() +
+![]() .якщо остання умова не виконується,то не існує кутів
.якщо остання умова не виконується,то не існує кутів![]() ,які б задовольняли умову(4)При цьому капля розтікається по поверхні
рідини.В даному випадку кажуть,що рідина 3 повністю змочується рідиною 2.
,які б задовольняли умову(4)При цьому капля розтікається по поверхні
рідини.В даному випадку кажуть,що рідина 3 повністю змочується рідиною 2.
Аналогічна ситуація,з каплею на твердому тілі. Різниця в тому,що тверда поверхня не може деформуватися. Кут визначається з формули:
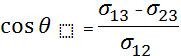 ;
;
Кут θ називається крайовим кутом. Зазвичай
його обирають так,щоб він включав в себе область зайняту рідиною2.Коли![]() >1,
>1, >
>![]() +
+![]() .
.
Але тоді не виконується умова cosθ=![]() .Капля рідини не знаходиться в рівновазі,а ростікається по поверхні
твердого тіла,покриваючи її тонкою плівкою.В цьому випадку говорять,що рідина повністю змочує поверхню твердого тіла. В
іншому випадку
.Капля рідини не знаходиться в рівновазі,а ростікається по поверхні
твердого тіла,покриваючи її тонкою плівкою.В цьому випадку говорять,що рідина повністю змочує поверхню твердого тіла. В
іншому випадку
![]() <-1,то також не існує ніякого кута θ,який би задовольняв
умову(1). Рідина в цьому випадку зтягується в сферичну каплю,дещо приплюснутою
силою тяжіння. В цьому випадку кажуть,що капля не змочує поверхність твердого тіла.В більшості випадків має місце
частичне змочування.
<-1,то також не існує ніякого кута θ,який би задовольняв
умову(1). Рідина в цьому випадку зтягується в сферичну каплю,дещо приплюснутою
силою тяжіння. В цьому випадку кажуть,що капля не змочує поверхність твердого тіла.В більшості випадків має місце
частичне змочування. 
71.Кривизна
поверхні і додатковий тиск . Формула Лапласа . Капілярні явища
Якщо поверхня рідини-крива , то при рівновазі
тиски по різні її сторони повинні бути різними . Явище
обумовлено силами поверхневого натягу. Розглянемо випадок коли рідина
 обмежена циліндром:
обмежена циліндром: ![]() - дотичні сили ,b -
довжина циліндра рівнодіюча сила:
- дотичні сили ,b -
довжина циліндра рівнодіюча сила: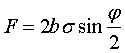
або ![]() ,
, 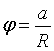 , де а- довжина дуги, отримаєм
, де а- довжина дуги, отримаєм
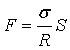 , де S=аb . Розділивши Силу F на площу S знайдемо різницю тисків всередині і назовні рідини
, де S=аb . Розділивши Силу F на площу S знайдемо різницю тисків всередині і назовні рідини
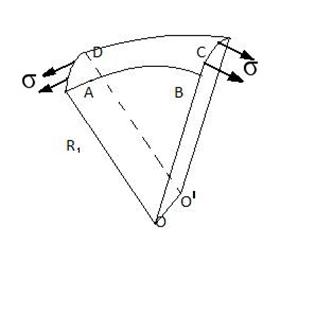
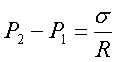 . 2. Узагальнимо цю формулу на
випадок ,коли рідина обмежена поверхнею подвійної кривизни
. 2. Узагальнимо цю формулу на
випадок ,коли рідина обмежена поверхнею подвійної кривизни
Тоді ![]() , де S –площа ABCD
, де S –площа ABCD
Результуюча дотичних сил рівна
![]() , де R2 , радіус AD
, де R2 , радіус AD
Результуюча всіх сил поверхневого натягу рівна:
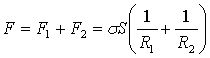
Розділивши її на S отримаємо
різницю. Тисків 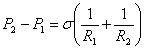 - формула Лапласа.
- формула Лапласа.
3. Якщо розміри посудин, в яких знаходиться рідина, або відстань між поверхнями , обмежуючих рідину , порівняні з радіусом кривизни поверхні рідини , то такі посудини називають капілярними , а явища , протікаючи в посудині, називають капілярними явищами .
В таких посудинах характерна дія додаткового
тиску (тиск Лапласа),за допомогою якого відбувається явище капілярного підйому,
а величина на яку підіймається рідина визначається за формулою: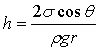
72.Капілярно-гравітаційні хвилі. (Доведення)
У випадку, коли одночасно діють сили тяжіння і сили поверхневого натягу,
хвилі називаються гравітаційно-капілярними. Вплив сил поверхневого натягу
найбільший при малих довжинах хвиль, сил тяжіння – при більших. Швидкість 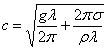 розповсюдження
хвиль на поверхні рідини залежить від довжини хвилі l. При довжини хвилі швидкість розповсюдження
гравітаційно-капілярних хвиль спочатку ¯ до деякого
мінімального значення
розповсюдження
хвиль на поверхні рідини залежить від довжини хвилі l. При довжини хвилі швидкість розповсюдження
гравітаційно-капілярних хвиль спочатку ¯ до деякого
мінімального значення ![]() , а потім (s - поверхневий натяг, g – прискорення
вільного падіння, r - густина рідини).
Значенню с1 відповідає довжина хвилі
, а потім (s - поверхневий натяг, g – прискорення
вільного падіння, r - густина рідини).
Значенню с1 відповідає довжина хвилі ![]() . При l > l1 швидкість розповсюдження залежить переважно від сил тяжіння
і не залежить від поверхневого натягу, тоді
. При l > l1 швидкість розповсюдження залежить переважно від сил тяжіння
і не залежить від поверхневого натягу, тоді 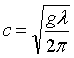 дані хвилі
називаються гравітаційними, а при l < l1 – від сил поверхневого натягу, де
дані хвилі
називаються гравітаційними, а при l < l1 – від сил поверхневого натягу, де 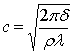 . Для поверхні
розділу води і повітря l1=1,71 см. Причини
виникнення гравітаційних хвиль: притягання рідини Сонцем і Місяцем, рух тіл
поблизу або на поверхні води (пароплавні хвилі), дія на поверхні рідини системи
імпульсних тисків
. Для поверхні
розділу води і повітря l1=1,71 см. Причини
виникнення гравітаційних хвиль: притягання рідини Сонцем і Місяцем, рух тіл
поблизу або на поверхні води (пароплавні хвилі), дія на поверхні рідини системи
імпульсних тисків
(місцеве підвищення рівня при підводному вибуху).
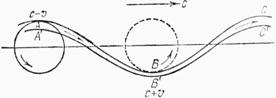 АВС-представляє
траєкторію частинки на поверхні рідини. А’В’С’-безкінечно близька до неї
частинки в глибині рідини.
АВС-представляє
траєкторію частинки на поверхні рідини. А’В’С’-безкінечно близька до неї
частинки в глибині рідини.
![]() -швидкість руху рідини в околі.
-швидкість руху рідини в околі.![]() -швидкість рідини в точці А.
-швидкість рідини в точці А. ![]() -повна швидкість в точці В. Різниця висот точок А та В
дорівнює h=2r. З рівняння Бенуллі:
-повна швидкість в точці В. Різниця висот точок А та В
дорівнює h=2r. З рівняння Бенуллі:
![]() або
або ![]()
Видно: 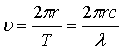 . Тиск рідини в точках А та В по формулі Лапласа рівні:
. Тиск рідини в точках А та В по формулі Лапласа рівні:
![]()
![]() , де К– абсолютне значення кривизни в точці А або В.
, де К– абсолютне значення кривизни в точці А або В.
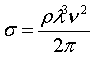
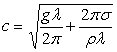
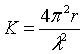 .Звідси
.Звідси
73.Кристалічний та аморфний стан речовини.
Належність речовини до кристалічного або аморфного стану визначається взаємним розташуванням атомів у ній.
У
кристалічній речовині атоми розташовані
впорядковано. Певний структурний елемент стало повторюється, утворюючи кристалічну структуру.
Атомна структура називається ідеальним кристалом, якщо в ній є три некомпланарних вектори a1,a2,a3, що утворюють праву трійку, при зсуві на кожний з яких вона не змінюється, тобто інварінтна. Зсув на кожний з таких векторів називається трансляцією.
Обєм паралелепіпеда, побудованого на цих векторах, буде дорівнювати мішаному добутку базових векторів, який можна записат як Ω=a1ּ۬[a2xa3]=a2ּ[a3xa1]=a3ּ[a1xa2] (1) Якщо вектори a1,a2,a3 вибрані таким чином, що обєм паралелепіпеда Ω має мінімально можливе значення, то ці вектори називають трансляційними або основними векторами трансляції, а побудований на них паралелепіпед-елементарною коміркою кристала. Якщо відомі основні вектори трансляції, можна знайти сукупність точок r’=r+n1a1+n2a2+n3a3, де r-довільна точка, а n(1,2,3)- довільні цілі числа(додатні відємні та нуль). Ця сукупність точок при довільних значеннях n утворює кристалічну гратку, самі точки мають назву вузлів кристалічної гратки. Кристалічна гратка є результатом усіх можливих трансляцій елементарної комірки і є сама по собі математичною абстракцією. Кристалічна структура утворюється лише тоді, коли з кожним вузлам гратки однаковим чином пов'язаний певний базис. Базисом може бути довільна сукупність атомів чи молекул, але завжди однакова біля кожного вузла. Головна асобливість внутрішньої будови тіл, що знаходяться у аморфному стані,- відсутність дальнього порядку, тобто характерної для кристалів повторюваності одного й того ж елементу структури. У аморфних речовин існує так званий ближній порядок, тобто деяка узгодженість у розташуванні у просторі сусідніх атомів, яка зникає із збільшенням відстані від вибраного атома.
Такі особливості розташування атомів зумовлюють фізичні властивості кристалів і аморфних тіл:
1) Кристалічні тіла анізотропні, чого повністю позбавлені аморфні тіла. Але анізотропію властивостей можна експериментально зафіксувати лише на дуже досконалих монокристалах. Найчастіше досліджуються полікристалічні речовини, де окремі монокристали розташовані в просторі хаотично. Тому, хоч кожний монокристал є анізотропним, полікристал буде ізотропним.
2)
Кристали мають правильну
геометричну форму. У всіх кристалах даної речовини за однакових умов кути між
відповідними гранями кристалів однакові. Це закон сталості кутів кристалу,
встановлений Стеноном у 1669 році на основі спостережень над багатогранними
кристалами у природі.
3)
Кристали, на відміну від аморфних
тіл, розколюються вздовж певних площин.
4)
Кристали, на відміну від аморфних
тіл, мають фіксовану температуру плавлення.
5)
І, найголовнішу, кристали мають
стійку симетрію
Елементи
симетрії кристалів
Симетрія-це властивість тіла суміщатися із самим собою під час деяких операцій або перетворень. Трансляційна симетрія є операцією, коли зсув всієї нескінчнної кристалічної гратки на основні вектори трансляції суміщає її із собою.
Наступні елементи симетрії мають назву точкових, оскільки при операції хоча б одна точка не змінює свого положення. При цьому, якщо трансляційна симетрія обовязкова для будь-якого кристала, ці елементи симетрії не є обовязковим атрибутом кожного кристала.
Вісь симетрії n-го порядку. Пряма, що проходить в кристалі, називається його віссю симетрії n-го порядку, якщо тіло суміщається із собою при вороті навколо цієї прямої на кут 360/n . кристал може мати осі симетрії 1,2,3,4 і 6-го порядків.
Дзеркальна площина. Якщо відображення від якоїсь площини переводить кожний вузол гратки в його дзеркальне зображення, то площина називається дзеркальною.
Центр інверсії. Нехай є деяка точка, від якої м ибудемо відраховувати радіус вектор r(x,y,z). Якщо тіло інваріантне операції r(x,y,z)=- r(-x,-y,-z) то точка відліку називається ценром інверсії.
Інверсійна вісь n-го порядку. Тіло суміститься із собою при повороті на кут 360/n навколо своєї осі і наступної інверсії щодо вузла, що лежить на цій осі.
Дзеркально-поворотна вісь n-го порядку. Тіло суміститься із собою при повороті навколо осі на кут 360/n і наступному дзеркальному відображенні в площині, перпендикулярній цій осі.
Сукупність точкових елементів симетрії, які має тіло, називається його точковою групою симетрії. Якщо до цих елементів чиметрії додати ще елементи симетрії, при яких жодна точка тіла не залишається нерухомою, наприклад, при трансляції на вектори гратки, то ми отримаємо просторову групу симетрії. Симетрія покладена в основу класифікації кристалів.
74. Просторові кристалічні гратки. Сингонії. Гратки Браве.
Напрямок, що не повторюється у кристалі, називається особливим. В залежності від кількості таких напрямків кристали поділяються на 3 категорії, які складаються з систем з однаковою точковою групою симетрії просторових граток - сингоній:
Вища категорія, напрямки відсутні. Відноситься лише одна сингонія-кубічна.
Середня категорія, єдиний особливий напрямок.Тетрагональна, тригональна і гексагональна сингонії.
Нижча категорія, декілька напрямків. Відносяться ромбічна, моноклінна,триклинна сингонії.
Трансляційна симетрія – властивість гратки суміщатися з собою після переміщення на основні вектори трансляції. Лише 14 точкових трьохвимірних структур можуть мати трансляційну симетрію. Ці просторові гратки називають гратками Браве.
75. Атомні площини. Індекси Міллера.
Атомною площиною кристалу називається площина, що проходить принаймні через три його атоми. Атомна площина ідеального кристалу містить нескінченне число атомів.
 Деяка площина проходить через 3 атоми кристали на осях системи
координат, відтинає відрізки
Деяка площина проходить через 3 атоми кристали на осях системи
координат, відтинає відрізки ![]() - цілі числа. Рівняння площини:
- цілі числа. Рівняння площини:
![]()
Складемо величини обернених відношень відтятих відрізків і виразимо його через найменші цілі числа:
Величини (![]() називають кристалографічними або індексами Міллера.
називають кристалографічними або індексами Міллера.
76 . Поверхнева енергія і зовнішня форма кристала . Закон Кюрі та Вульфа .
Кристали можуть мати рівноважну і нерівноважну
форму . Кристал рівноважної форми – той , що не змінює свою форму у
власному розплаві , при температурі
плавлення що відповідає сталому тискові , або при заданих температурі і тискові
у насиченому розчині . Згідно з принципом Кюрі та Вульфа , кристал рівноважної
форми повинен при заданому об’ємі ![]() мати мінімальну
поверхневу енергію.
мати мінімальну
поверхневу енергію.
Поверхнева енергія – це надлишок енергії поверхневого шару на межі розділу фаз, зумовлений різницею між молекулярної взаємодії в обох фазах. Робота, що витрачається на створення одиниці площі поверхні розділу фаз у оборотному езотермічному процесі визначає питому вільну поверхневу енергію, яка визначається рівнянням Гіббса-Гельмгольца.
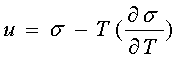
![]() - коефіцієнт поверхневого натягу
- коефіцієнт поверхневого натягу
Закон Кюрі-Вульфа
![]()
Якщо поверхневий натяг на одній із граней набагато більший, ніж на іншій, то вона буде швидше рости , отже відстані до грані зростуть з принципом Кюрі-Вульфа, . Кінець- кінцем гран із більшим натягом заросте.
77. Класифікація кристалів за типами зв’язку в кристалічній гратці.
Іонний зв'язок досить сильний. Він становить величину порядку 105 Дж/моль. Міцність іонного зв'язку проявляється в тому, що іонні кристали мають малий коефіцієнт теплового розширення і високу температуру плавлення. Електропровідність іонних кристалів при кімнатних температурах дуже незначна. Вона на 20 порядків нижча, ніж металів, і зростає з підвищенням температури. Для іонних кристалів характерним є сильне поглинання в інфрачервоній області спектра. Типовими кристалами з ковалентним зв'язком є алмаз, графіт, карборунд, сульфід цинку, йод, сірка. До них належать і напівпровідники. У вузлах кристалічної решітки таких кристалів розміщені нейтральні атоми.
Основу ковалентного зв'язку становить обмінний ефект, зумовлений обміном електронами між атомами. Ковалентний зв'язок між двома атомами може здійснюватись однією парою електронів (одинарний зв'язок); двома парами (подвійний зв'язок); трьома парами електронів (потрійний зв'язок). Ковалентний зв'язок досить сильний. Тому ковалентні кристали мають велику енергію зв'язку порядку 3—5 еВ на один атом. Завдяки цьому кристали з ковалентними зв'язками мають високу механічну міцність і твердість, високу температуру плавлення, винятково малу леткість, погану електропровідність в широкому інтервалі температур.
Металічний зв'язок в основному характерний для речовин, побудованих з атомів одного елемента (наприклад, мідь, золото). Металічні кристали містять у вузлах кристалічної решітки позитивні іони. Металічний зв'язок здійснюється не через електронні пари, які сумісно належать двом частинкам, а за допомогою вільних валентних електронів, що належать всьому кристалу в цілому. Енергія металічного зв'язку значно менша, ніж у ковалентних і іонних кристалів. Підтвердженням цього є більш низька температура плавлення металів, ніж іонних і ковалентних кристалів. Висока концентрація вільних електронів у металів зумовлює їхню добру електро - та теплопровідність. Метали оптично непрозорі, мають велику відбивну здатність, тому для них характерний специфічний металічний блиск.
У вузлах кристалічних решіток молекулярних кристалів розміщаються певним способом орієнтовані молекули. Характерною для молекулярних кристалів є геометрична відокремленість молекул кристала і сильні внутрішньомолекулярні зв'язки. Це означає, що енергія внут-рішньомолекулярних зв'язків значно перевищує енергію міжмолекулярних зв'язків. Силами зв'язку в цьому разі є сили Ван-дер-Ваальса та водневі зв'язки, коли молекули мають гідроксильні ОН та амінні NH2 групи. Переважна більшість молекулярних кристалів — це органічні кристали. Молекулярні неорганічні кристали трапляються рідко. До них належать речовини, молекули яких складаються з азоту, фосфору, сірки та ін. Молекулярні кристали за фізичними властивостями є ізоляторами, мають низьку температуру плавлення, прозорі для широкого інтервалу електромагнітних хвиль.
Зауважимо, що практично немає речовин, які б характеризувались тільки одним типом зв'язків. Здебільшого кристалічним решіткам речовин властива одночасна дія різних типів зв'язку.
78. Дефекти кристалічної гратки. Дефекти за Шотткі і за Френкелем. Температурна залежність концентрації.
Будь-яке порушення періодичності кристалічної структури
структури називається дефектом. Найпростішим дефектом кристалічної гратки є
вакансія(рис.), яка являє собою вузол кристалічної гратки, в якому
відсутній атом. Цей дефект називається дефектом Шотткі. Іншим точковим
дефектом є дефект за Френкелем. Він являє собою пару вакансія + атом у міжвузлі. Число вакансій у кристалі залежить від температури. Із
збільшенням температури вони рухаються переважно із поверхні в об’єм, а при
зниженні – навпаки, із об’єму на поверхню. Утворення точкового дефекту
вимагає затрат енергії, отже з енергетичної точки зору може здаватись
невигідним. Але при фіксованій температурі Т умовою рівноваги для кристалу
згідно з принципом Кюрі-Вульфа є стан з мінімальною вільною енергією
при сталому об’ємі F = U – TS. Збільшення числа
вакансій збільшує ентропію S, тому зменшує вільну енергію.

79.Теплоємність твердих тіл. Закони Дюлонга і Пті та Джоуля і Каппа. Недоліки класичної теорії теплоємності твердих тіл.
Тверде тіло розглядається як набір
класичних осциляторів. На один ступінь вільності коливального руху припадає
енергія рівна kT. Внутрішня енергія одного моля твердого тіла U =3NkT= 3RT. Молярна теплоємність ![]() . Тобто не залежить від температури є однаковим для всіх твердих тіл (Закон
Дюлонга і Пті ). Недоліки : цей закон не підтверджується при низьких
температурах, а для деяких твердих тіл – і при деяких високих. Експеримент
свідчить :
. Тобто не залежить від температури є однаковим для всіх твердих тіл (Закон
Дюлонга і Пті ). Недоліки : цей закон не підтверджується при низьких
температурах, а для деяких твердих тіл – і при деяких високих. Експеримент
свідчить : ![]() . Якщо тверде тіло є хімічною
сполукою, тобто його кристалічна ґратка складається з атомів різних типів, на
кожен атом усе-одно припадає 3 коливальні ступені вільності, отже, на молекулу
припадає енергія 3nkT, де n— кількість атомів у молекулі. Отже, має місце
формула C=3nR – закон Джоуля-Каппа . Вона більш загальна, ніж Дюлонга-Пті.
. Якщо тверде тіло є хімічною
сполукою, тобто його кристалічна ґратка складається з атомів різних типів, на
кожен атом усе-одно припадає 3 коливальні ступені вільності, отже, на молекулу
припадає енергія 3nkT, де n— кількість атомів у молекулі. Отже, має місце
формула C=3nR – закон Джоуля-Каппа . Вона більш загальна, ніж Дюлонга-Пті.
80. Квантова теорія теплоємності твердих тіл Планка-Енштейна.
Тверде тіло Розглядається як сукупність
незалежних осциляторів, енергія яких може набувати лише дискретних значень
E=nhv , де n – ціле число, h – стала Планка , v – частота. Всі осцилятори мають однакову
частоту v. Середня енергія осцилятора: ![]() , де
, де ![]() -- енергія нульових коливань осцилятора.
Внутрішня енергія 1 моля твердого тіла : U=3N
-- енергія нульових коливань осцилятора.
Внутрішня енергія 1 моля твердого тіла : U=3N![]() , а молярна теплоємність :
, а молярна теплоємність : 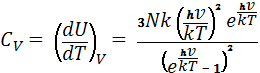 . Ця
формула дає правильний результат при
. Ця
формула дає правильний результат при ![]() . Тоді
. Тоді ![]() , що узгоджується з
тепловою теоремою Нернста і експериментом. Але загальний хід залежності
, що узгоджується з
тепловою теоремою Нернста і експериментом. Але загальний хід залежності
![]() при
низьких температурах формула дає експоненціальний, на відміну від
експериментального :
при
низьких температурах формула дає експоненціальний, на відміну від
експериментального :
![]()
81. Квантова теорія теплоємності твердих тіл Дебая-Борна . Температура Дебая.
Зміщення атомів представляється як система поздовжніх та поперечних хвиль суцільного однорідного твердого тіла. Система хвиль має широкий спектр частот. Всі хвилі з будь-якими частотами малої відповідають поперечним і поздовжнім хвилям у твердому тілі( тобто нехтуємо дисперсією хвиль). Внутрішня енергія 1 моля твердого тіла та молярна теплоємність:
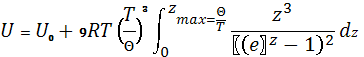
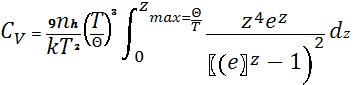 , де
, де
z=![]() , де n — кількість атомів у
одиниці об’єму,
, де n — кількість атомів у
одиниці об’єму, ![]() – температура Дебая. Теорія
Дебая-Борна дає температурну залежність теплоємності
– температура Дебая. Теорія
Дебая-Борна дає температурну залежність теплоємності ![]() при низьких температурах, що
узгоджується із експериментом. При високих температурах теплоємність набуває
сталого значення, яке передбачає класична теорія.
при низьких температурах, що
узгоджується із експериментом. При високих температурах теплоємність набуває
сталого значення, яке передбачає класична теорія.
Температура
Дебая - температура, при якій збуджуються всі моди коливань у даному твердому
тілі. Подальше збільшення температури не призводить до появи нових мод
коливань, а лише веде до збільшення амплітуди вже існуючих, тобто середня
енергія коливань із зростанням температури зростає. Температура Дебая - фізична
константа речовини, що характеризує багато властивостей твердих тіл -
теплоємність, електропровідність, теплопровідність, збільшення ширини ліній
рентгенівських спектрів, пружні властивості і т. п. Введена вперше П. Дебаем в
його теорії теплоємність. Температура Дебая визначається наступною формулою: Θd=hVdk, де h - постійна Планка, ![]() - максимальна
частота коливань атомів твердого тіла, k - постійна Больцмана. Температура
Дебая наближено вказує температурний кордон, нижче якої починають впливати
квантові ефекти.
- максимальна
частота коливань атомів твердого тіла, k - постійна Больцмана. Температура
Дебая наближено вказує температурний кордон, нижче якої починають впливати
квантові ефекти.
83. Кипіння та конденсація на ядрах.. Камера Вільсона, бульбашкова камера.
Для виникнення конденсації необхідна наявність центрів конденсації, які захоплюють підлітаючі до них молекули. Центрами конденсації можуть бути порошинки, краплі рідини, заряджені частинки (іони). Є два режими конденсації: поверхнева, капельна. Конденсація може відбуватися всередині об’єму пари. Для початку такої конденсації пара повинна бути пересичена.
На цьому принципі побудована камера Вільсона. Вона представляє собою ємність, розділену на дві об’єднані між собою поршнем. Об’єм поршнем наповнений газом, що містить насичені пари довільної рідини. Якщо швидко опустити поршень, то суміш адіабатично розшириться і охолодиться. Пара при цьому стане пересиченою, але конденсуватися не буде, тому що забезпечується відсутність центрів конденсації в камері. Але якщо в момент розширення камери крізь неї пролетить швидка частинка, що здатна іонізувати атоми, то на її шляху з’явиться намисто іонів. На цих іонах, як на центрах, почнеться конденсація парів і утворення крапель туману. Таким чином досліджуються частинки космічних променів і ядерні частинки. Бульбашкова камера така ж, тільки суміш – перегріта рідина, спостерігається кипіння.
84. Фазові переходи II роду. Співвідношення Ернста
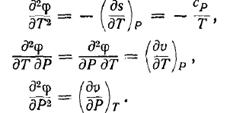 Фазовими перетвореннями II роду назваються такі перетворення, при яких перші похідні від функції
термодинамічного потенціалу залишаються неперервними, а другі похідні
змінюються скачкоподібно. Це значить що ФП II роду не супроводжуються виділенням або поглинанням
тепла а також зміною питомого об’єму речовини. З розривності других слідує, що
при ФП II роду скачко
подібно змінюється одна з величин (див. формули):
Фазовими перетвореннями II роду назваються такі перетворення, при яких перші похідні від функції
термодинамічного потенціалу залишаються неперервними, а другі похідні
змінюються скачкоподібно. Це значить що ФП II роду не супроводжуються виділенням або поглинанням
тепла а також зміною питомого об’єму речовини. З розривності других слідує, що
при ФП II роду скачко
подібно змінюється одна з величин (див. формули):
- питома теплоємність ср;
- коефіцієнт теплового розширення 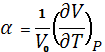 ;
;
- ізотермічний коефіцієнт стиснення 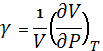 ;
;
Співвідношення Ернста - наслідок неперервності питомої ентропії S і питомого об’єму V.
Воно має вид: ![]() , тут
, тут ![]() означають стрибки при фазових перетвореннях.
означають стрибки при фазових перетвореннях.
85. Рідкі розчини. Закон Генрі. Закон Рауля. Наслідки з них.
Розчином називають фізично однорідні (гомогенні) суміші двох або більше речовин. Однорідність досягається рівномірним перемішуванням молекул. Якщо однієї з речовин у суміші більше, вона називається розчинником, а інші речовини суміші-розчиненими речовинами.
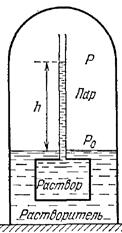 Закон Рауля
Закон Рауля
Нехай розчин поміщено в осмометр і вся система знаходиться під ковпаком.
Р0, Р-тиск насиченої пари над поверхнею рідини в ковпаку і в трубці.
Очевидно що
Р0-Р=.
Таким чином маємо:
, де ![]() - кількість молекул пари, n-розчинника в одиниці об’єму. Врахувавши, що
- кількість молекул пари, n-розчинника в одиниці об’єму. Врахувавши, що 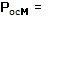 n′kT (закон Вант-Гоффа, n′- кількість молекул розчиненої речовини в
одиниці обєму),
n′kT (закон Вант-Гоффа, n′- кількість молекул розчиненої речовини в
одиниці обєму), ![]() маємо:
маємо:
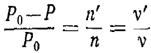 Відносне пониження тиску насиченої пари розчинника
над поверхнею слабкого розчину нелеткої речовини рівне віднощенню числа молей
розчиненої речовини до числа молей розчинника.
Відносне пониження тиску насиченої пари розчинника
над поверхнею слабкого розчину нелеткої речовини рівне віднощенню числа молей
розчиненої речовини до числа молей розчинника.
Закон Генрі
Був виведений
експериментально. Формулювання: при
незмінній температурі розчинність газу прямопропорційна його парціальному тиску
над поверхнею розчину.
86. Осмос. Осмотичний тиск. Закон Вант-Гоффа. Вплив дисоціації під час розчинення на осмотичний тиск.
Нехай розчин знаходиться у деякій посудині, відділений від чистого розчинника полупроникною перегородкою, крізь яку можуть проходити молекули розчинника, але не проходять молекули розчиненої речовини. Крізь таку перегородку молекули чистого розчинника переходитимуть в область зайняту розчином. Це явище називається осмосом. В результаті осмосу виникає різниця тисків між розчином і чистим розчинником. Коли вона досягає певного значення, осмос припиняється. Різниця тисків, при якій осмос припиняється називається осмотичним тиском.
Закон Вант-Гоффа: якщо розчин слабий, то кількість ударів молекул розчиненої речовини об стінку буде такою ж, як і для ідеального газу. Таким чином для осмотичного тиску
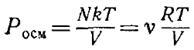 Тут N, v – числа молекул і молей
розчиненї речовини в об’ємі V.
Тут N, v – числа молекул і молей
розчиненї речовини в об’ємі V.
В розчинах електролітів може відбуватись дисоціація (розпад на йони) молекул, через що осмотичний тиск стає більшим, ніж розрахований по формулі. Проте, якщо під N розуміти загальну кількість часток в розчині, формула знову стає вірною.
..
…
…
…