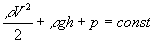 . Це є рівняння
Бернуллі.
. Це є рівняння
Бернуллі.Стаціонарна течія рідин. Трубка току. Рівняння нерозривності. Рівняння Бернуллі. Динамічний тиск. Течія рідини в трубах. В’язкість рідини. Закон Пуазейля. Ламінарні та турбулентні потоки. Число Рейнольдса.
12.1. Гідродинаміка представляє собою розділ механіки суцільних середовищ, в якому вивчається рух нестискаємих рідин та взаємодія цих рідин з твердими тілами.
12.2. Стан руху рідини можна визначити, якщо вказати для кожної точки простору вектор швидкості V, як функцію часу. Сукупність векторів V, заданих для всіх точок простору, утворює поле векторів швидкості.
12.3. Проведемо в рухомій рідині лінії так, щоб дотична до них в кожній точці співпадала по напрямку з вектором V. Ці лінії називаються лініями струму.
12.4. Домовимося проводити лінії струму так, щоб щільність їх (яка характеризується відношенням числа ліній D N до величини перпендикулярної їм площі D S, через яку вони проходять) була пропорційна до величини швидкості точки в даному місці. Тоді по картині ліній струму можна судити не лише про напрямок, а також про модуль вектора V в різних точках простору. Там, де швидкість більша, лінії струму будуть проходити щільніше, а там, де менша, – рідше.
12.5. Якщо вектор швидкості в кожній точці залишається постійним з плином часу, то потік рідини називається усталеним або стаціонарним.
12.6. Частина рідини, обмежена лініями струму, називається трубкою струму.
12.7. Для нестискуваної рідини величина SV в будь-якому перерізі однієї й тієї ж трубки струму є постійною. Це є теорема про неперервність струменя.
12.8. Рідина, в якій внутрішнє тертя (в`язкість) повністю відсутнє, називають ідеальною.
12.9. В стаціонарно текучій ідеальній рідині вздовж будь-якої лінії струму
виконується умова: 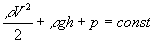 . Це є рівняння
Бернуллі.
. Це є рівняння
Бернуллі.
12.10. Тиск менше в точках, де швидкість більша.
12.11. Швидкість витікання рідини з отвору, який розміщено на глибині h під поверхнею, співпадає з швидкістю, яку набуде будь-яке тіло, що падає з висоти h.
12.12. Ідеальна рідина, тобто рідина без тертя, є абстракцією. Всім реальним рідинам та газам в більшій чи меншій мірі властива в’язкість – внутрішнє тертя. В’язкість проявляється в тому, що збуджений в рідині чи газі рух після усунення причин, які його збудили, поступово припиняється.
12.13. Розглядаючи взаємодію між двома паралельними пластинами в деякому середовищі, де одна пластина закріплена, а друга рухається, можна дослідити залежність сили взаємодії від характеристик системи.
Варіюючи швидкість пластини V0,
площу S та відстань між ними d,
можна отримати, що сила взаємодії між ними 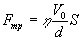 ,
де h – коефіцієнт
пропорційності, який залежить від природи та стану (наприклад температури) рідини
і називається коефіцієнтом внутрішнього тертя або коефіцієнтом
в`язкості, або просто в’язкістю рідини.
,
де h – коефіцієнт
пропорційності, який залежить від природи та стану (наприклад температури) рідини
і називається коефіцієнтом внутрішнього тертя або коефіцієнтом
в`язкості, або просто в’язкістю рідини.
Ця формула визначає не лише силу тертя, яка діє на пластину, але і силу тертя між шарами рідини, що контактують.
12.14. Одиницею в’язкості в системі СІ служить така в’язкість, при якій градієнт швидкості з модулем 1м/с приводить до виникнення сили тертя в 1 Н на 1 м2 поверхні дотику шарів. Ця одиниця називається паскаль-секунда, в СГС – пуаз. 1 Па.с. = 10 П .
12.15. Спостерігаються два види течії рідини (або газу). В одному випадку
рідина ніби-то розділяється на шари, які ковзають один відносно одного, не перемішуючись.
Така течія називається ламінарною
(шаруватою). Частинки рідини в ламінарному потоці не переходять з одного шару
в інший. Ламінарний потік стаціонарний.
При збільшенні швидкості чи різкій зміні поперечних розмірів струменя характер
течії, через взаємодії рідини із стінками посудини, суттєвим чином змінюється.
Виникає енергійне перемішування рідини. Така течія називається турбулентною.
При турбулентній течії швидкість частинок в кожному даному місці весь
час змінюється невпорядкованим чином – течія нестаціонарна.
Обтікання тіл рідиною або газом. Лобовий опір і підіймальна сила. Ефект Магнуса. Формула Жуковського.
12.16. Результуючу силу взаємодії тіла із струменем рідини чи газу можна розкласти
на дві складові: складова по струменю називається лобовим
опором.
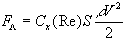 .
.
Сl ,
яка залежить від Re , називається коефіцієнтом лобового
опору.
12.17. Існують три причини виникнення лобового опору: