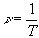9. Коливання

Гармонічні коливання. Рівняння руху та його розв’язок. Амплітуда, частота, фаза. Власні коливання: математичний та фізичний маятники, пружний маятник, коливальний контур. Енергія коливань. Запис гармонічних коливань у комплексній формі. Додавання коливань. Биття. Фігури Лісажу.

9.1. Коливання – це процеси, які точно або наближено повторюються через однакові проміжки часу.

9.2. Механічні коливання – зміни положення та швидкостей тіл або їх частин, що повторюються в часі.

9.3. Електричні коливання – періодичні зміни напруг та сил струмів в електричних колах і напруженостей електричних та магнітних полів навколо них.

9.4. Вільні (власні) коливання відбуваються самі по собі в системі, яка виведена зі стану рівноваги. Вони визначаються виключно властивостями системи.

9.5. Вимушені коливання відбуваються під дією сили, яка змінюється з часом.

9.6. Автоколивання відбуваються в системі, яка сама регулює додавання енергії від зовнішнього джерела (наприклад, маятник годинника з анкерним механізмом).

9.7. Параметричні коливання – такі, при яких відбувається періодична зміна якогось параметра коливальної системи з часом (наприклад, довжини математичного маятника). Це застосовується для поповнення енергії такої системи, що може бути втрачена за рахунок тертя.

9.8. Величину найбільшого відхилення системи від положення рівноваги називають амплітудою коливань.

9.9. Величину w ₀t+j ₀, що стоїть під знаком синуса, називають фазою коливань. Постійна j ₀ – це значення фази в момент часу t = 0 і називається початковою фазою коливань. Її значення визначається вибором початку відліку часу.

9.10. Оскільки синус – періодична функція з періодом 2p , то різні стани системи, яка здійснює гармонічні коливання, повторюються через такі проміжки часу Т, за які фаза системи отримує приріст, рівний 2p. Цей проміжок часу називають періодом коливань.

9.11. Число коливань в одиницю часу називають частотою коливань .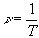
Кругова частота коливань w ₀= 2p n  – це число коливань за 2p секунд.

9.12. Маятник – тверде тіло, яке здійснює коливання навколо нерухомої осі або точки.

9.13. Математичним маятником називають ідеалізовану систему, що складається з нерухомої і нерозтяжної нитки, на якій підвішена маса, зосереджена в одній точці.

9.14. Фізичним маятником зветься тверде тіло, яке підвішене на нерухомій горизонтальній осі в полі тяжіння.

9.15. Приведена довжина фізичного маятника – це довжина такого математичного маятника, який має той же самий період коливань і ту ж масу, що і даний фізичний маятник.

9.16. Гармонічні коливання можуть бути представлені за допомогою вектора , що обертається.

Проекція кінця вектора на вісь буде здійснювати гармонічні коливання з амплітудою, яка дорівнює довжині вектора, з круговою частотою, рівною кутовій швидкості обертання вектора, і початковою фазою, яка дорівнює куту, що утворюється між віссю ОХ та вектором в початковий момент часу.

9.17.Представлення гармонічних коливань за допомогою векторів дає змогу звести додавання коливань до додавання векторів.

9.18.Представлення гармонічних коливань за допомогою комплексних змінних
       

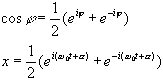
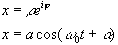
9.19. При додаванні двох коливань одного напрямку, які мало відрізняються по частоті, відбувається рух гармонічного типу з пульсуючою амплітудою. Такі коливання називаються биттям.

9.20. При додаванні коливань, що відбуваються у взаємоперпендикулярних напрямках утворюються фігури Лісажу.

Затухаючі коливання. Рівняння руху та їх рішення. Декремент затухання. Добротність.

9.21. При присутності тертя, що є зовнішньою силою, енергія коливань лінійного осцилятора зменшується, а отже зменшується і амплітуда коливань. Коливання при присутності тертя стають затухаючими.

9.22. Сила тертя діє проти швидкості. Отже, для лінійного осцилятора її дія еквівалентна зменшенню повертаючої сили, тобто пружності пружини. Оскільки 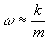, то це означає, що частота коливань має зменшуватися, а період – збільшуватися.

9.23. Швидкість затухання коливань визначається величиною 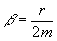, яку називають коефіцієнтом затухання.

9.24. Відношення значень амплітуд відповідних моментів часу, які відрізняються на період, називають декрементом затухання, а його логарифм – логарифмічним декрементом затухання. Логарифмічний декремент затухання обернений по величині числу коливань, здійснених за той час, за який амплітуда зменшилась в e разів.

9.25. Для характеристики коливань використовують величину 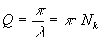, яку називають добротністю системи, що коливається. Добротність пропорційна числу коливань N_k, здійснених за той час t , за який амплітуда зменшилася в e разів.

Вимушені коливання. Рівняння руху та його рішення. Амплітудно-частотна та фазо-частотна характеристики. Резонанс.

9.26. Коливання, що здійснюються під постійною дією періодичної зовнішньої сили називаються вимушеними. Під дією гармонічної зовнішньої сили осцилятор здійснює вимушені гармонічні коливання з частотою цієї сили. Фаза та амплітуда цих коливань визначається як зовнішньою силою, так і характеристиками осцилятора.

9.27. Крива, що описує залежність амплітуди вимушених усталених коливань від частоти зовнішньої сили називається амплітудно-частотною характеристикою.

9.28. Максимальне значення амплітуда досягає при частоті зовнішньої сили близької до власної частоти осцилятора (w » w ₀). Коливання з максимальною амплітудою називаються резонансними, а саме явище "розкачки" коливань до максимальної амплітуди при w » w ₀ – резонансом. Частота w ₀  в цьому випадку називається резонансною.

9.29. Співвідношення фаз вимушених коливань і вимушуючої сили може бути різним. Залежність цієї різниці фаз j від частоти вимушуючої сили називається фазово-частотною характеристикою.

9.30. При дуже малих частотах w<< w ₀  фаза j мала і від`ємна. Це означає, що зміщення відстає по фазі від сили на дуже невелику величину; з ростом частоти відставання зміщення по фазі від сили збільшується. При резонансі зміщення відстає від сили по фазі на кут 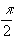. Це означає, що в момент, коли сила досягає максимального значення, зміщення дорівнює нулю і навпаки, коли сила – нуль, то зміщення максимальне. При подальшому рості частоти відставання від сили продовжує збільшуватись, і при дуже великих частотах w > > w ₀  наближається до p . Можна казати, що сила і зміщення напрямлені в протилежні сторони. Тому, коли, наприклад, сила досягає максимального додатного значення, то зміщення – максимального від’ємного і навпаки.

9.31. При резонансі швидкість випереджує зміщення н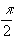а ; сила теж випереджує зміщення на той же кут. Отже при резонансі швидкість та сила коливаються в одній фазі, тобто сила весь час співпадає по напрямку зі швидкістю. Тому робота зовнішньої сили досягає максимального значення. Якщо резонанс відсутній, то частину часу сила напрямлена проти швидкості, а, отже, енергія осцилятора зменшується, а частину часу – за швидкістю, і енергія збільшується. Тому резонанс характеризується наявністю найбільш сприятливих умов для передання енергії від зовнішнього джерела до осцилятора.

Розкладання коливань на гармонічні складові. Фур’є-аналіз. Спектр коливань. Автоколивання. Параметричне збудження коливань. Поняття про нелінійні коливання.

9.32. Реальні коливання не є гармонічними. Але їх можна представити як суму гармонічних коливань, а саме коливань з кратними частотами. Ці гармонічні коливання, що складають будь-яке реальне коливання звуть гармоніками.

9.33. Математичний метод розкладання складного коливання на гармоніки полягає в розкладанні функції в ряд Фур’є. Повний перелік гармонік, що дає амплітуду, частоту і фазу кожної називають спектром Фур’є. Цей спектр ілюструють за допомогою діаграми, в якій по вісі ординат вказано масштаб амплітуди, а по вісі абсцис – масштаб частоти гармонік. Кожній гармоніці відповідає відрізок, перпендикулярний до вісі абсцис в точці, що вказує частоту гармоніки. Довжина відрізка вказує амплітуду гармоніки.

9.34.Найбільш суттєвою особливістю розв`язку рівняння руху при наявності збурення є присутність члена з 2w . Це показує, що завдяки наявності в силі нелінійного члена, пропорційного x², в коливаннях з’явиться член з подвоєною частотою, що називається другою гармонікою. Якщо продовжити розв’язок і знайти наступні, маліші поправки, то можна переконатися, що вони мають більш високі частоти nw ₀, кратні основній, або, іншими словами, вищі гармоніки. Тому найбільш характерний наслідок наявності нелінійності в силі – це виникнення вищих гармонік в коливаннях.